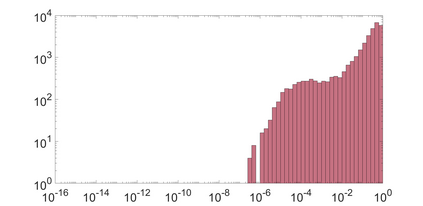
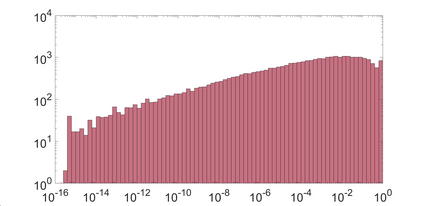
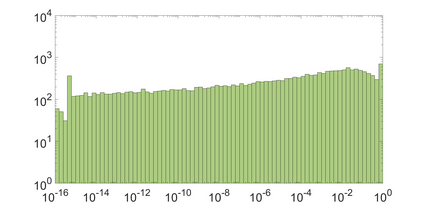
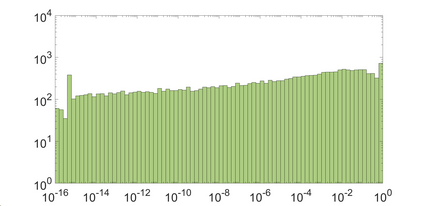
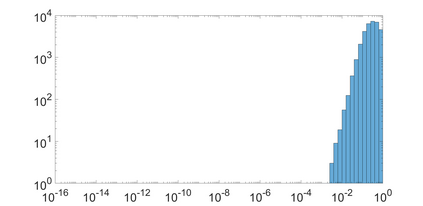
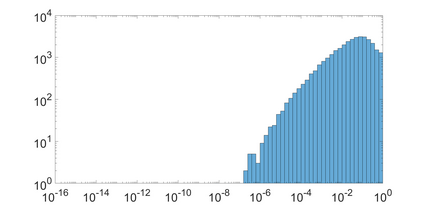
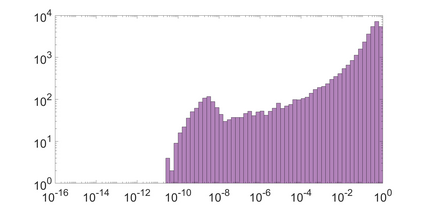
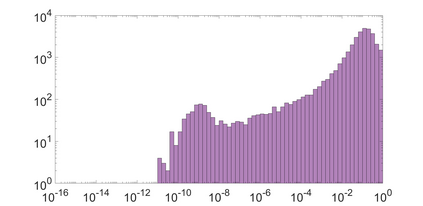
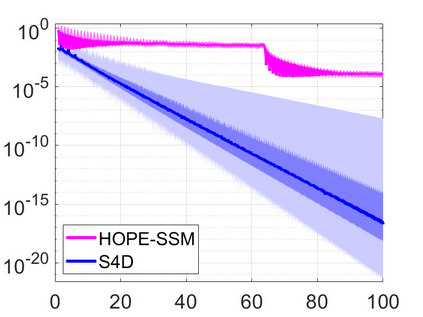
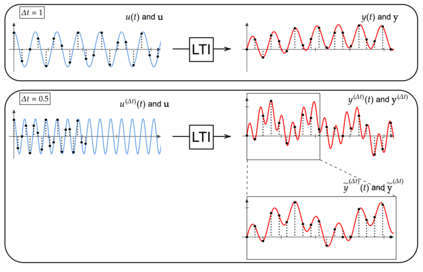
State-space models (SSMs) that utilize linear, time-invariant (LTI) systems are known for their effectiveness in learning long sequences. To achieve state-of-the-art performance, an SSM often needs a specifically designed initialization, and the training of state matrices is on a logarithmic scale with a very small learning rate. To understand these choices from a unified perspective, we view SSMs through the lens of Hankel operator theory. Building upon it, we develop a new parameterization scheme, called HOPE, for LTI systems that utilizes Markov parameters within Hankel operators. Our approach helps improve the initialization and training stability, leading to a more robust parameterization. We efficiently implement these innovations by nonuniformly sampling the transfer functions of LTI systems, and they require fewer parameters compared to canonical SSMs. When benchmarked against HiPPO-initialized models such as S4 and S4D, an SSM parameterized by Hankel operators demonstrates improved performance on Long-Range Arena (LRA) tasks. Moreover, our new parameterization endows the SSM with non-decaying memory within a fixed time window, which is empirically corroborated by a sequential CIFAR-10 task with padded noise.
翻译:暂无翻译