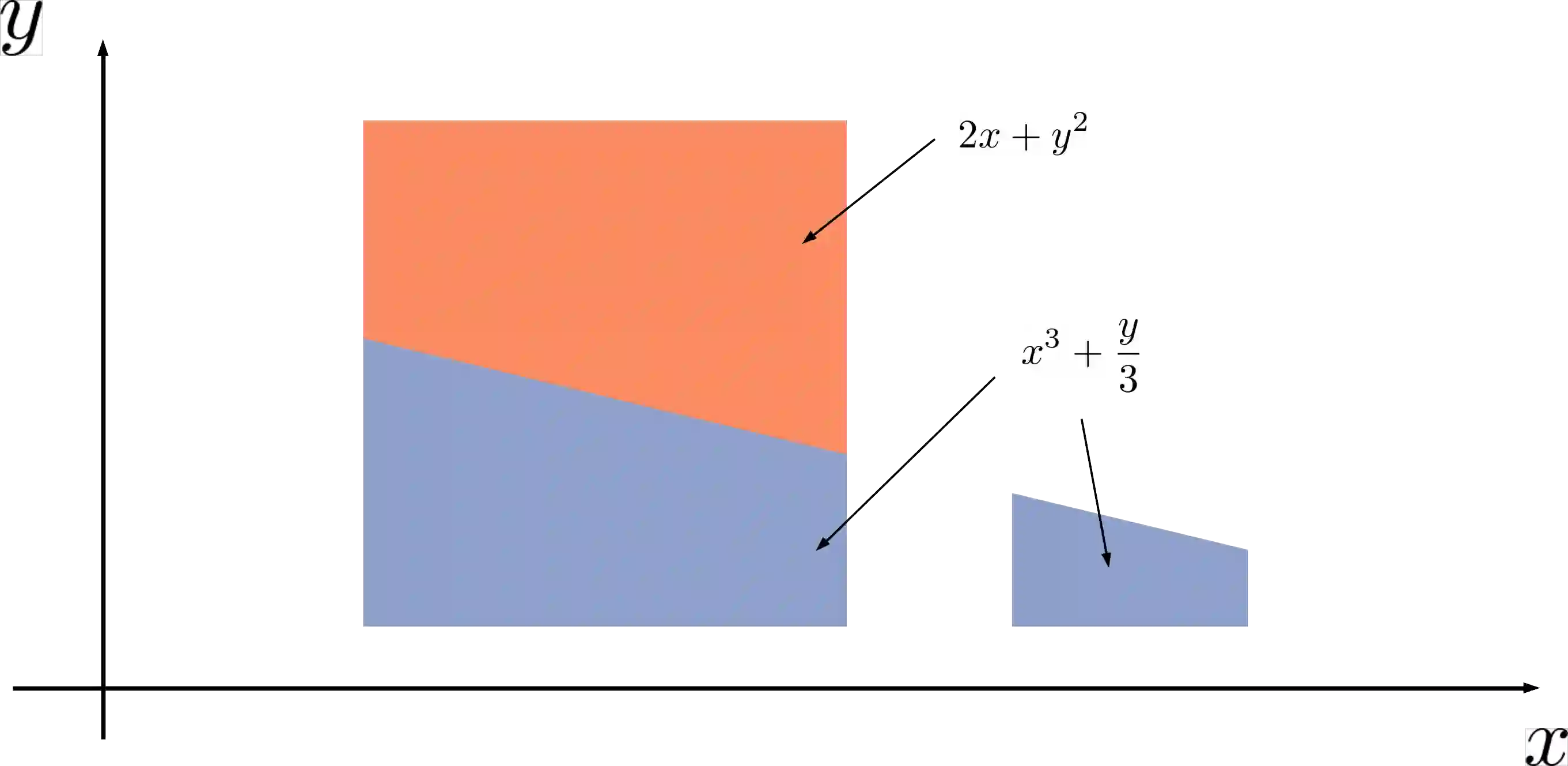
Weighted model counting (WMC) is a popular framework to perform probabilistic inference with discrete random variables. Recently, WMC has been extended to weighted model integration (WMI) in order to additionally handle continuous variables. At their core, WMI problems consist of computing integrals and sums over weighted logical formulas. From a theoretical standpoint, WMI has been formulated by patching the sum over weighted formulas, which is already present in WMC, with Riemann integration. A more principled approach to integration, which is rooted in measure theory, is Lebesgue integration. Lebesgue integration allows one to treat discrete and continuous variables on equal footing in a principled fashion. We propose a theoretically sound measure theoretic formulation of weighted model integration, which naturally reduces to weighted model counting in the absence of continuous variables. Instead of regarding weighted model integration as an extension of weighted model counting, WMC emerges as a special case of WMI in our formulation.
翻译:加权模型计数(WMC)是一个对离散随机变量进行概率推算的流行框架。最近,WMC被扩大到加权模型集成(WMI),以便进一步处理连续变量。在其核心方面,WMI问题包括计算整体和加权逻辑公式的总和。从理论角度讲,WMI是通过在WMC中已经存在的加权公式总和与Riemann整合相匹配来拟订的。基于计量理论的更有原则的一体化方法是Lebesgue集成。Lebesgue集成允许以有原则的方式对离散和连续变量进行同等处理。我们提出了一个加权模型集成的理论合理的计量公式,在没有连续变量的情况下,这自然会减为加权模型计数。在加权模型计数的延伸中,WMC没有作为加权模型集成的延伸,而是在我们公式中作为WMI的一个特殊案例出现。