Pointwise Maximal Leakage

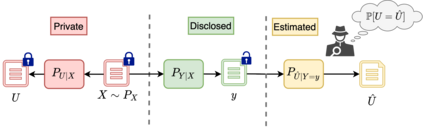
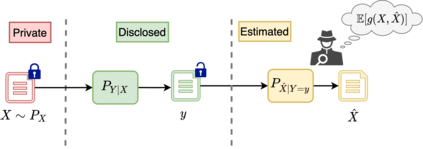
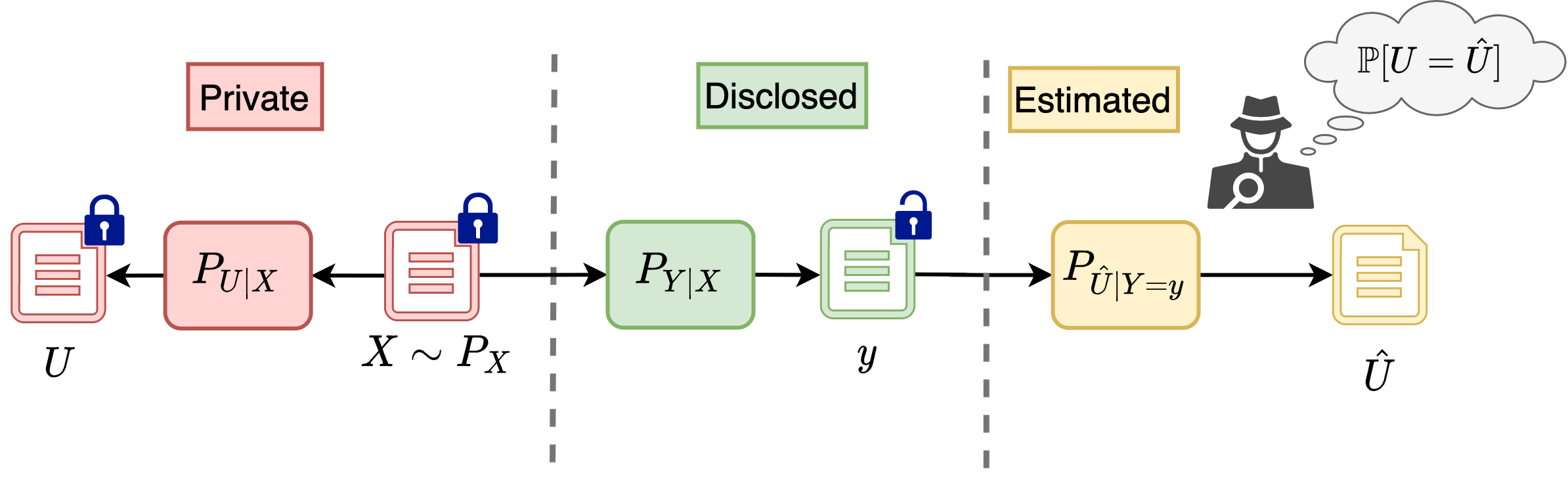
We introduce a privacy measure called pointwise maximal leakage, defined based on the pre-existing notion of maximal leakage, which quantifies the amount of information leaking about a secret $X$ by disclosing a single outcome of a (randomized) function calculated on $X$. Pointwise maximal leakage is a robust and operationally meaningful privacy measure that captures the largest amount of information leaking about $X$ to adversaries seeking to guess arbitrary (possibly randomized) functions of $X$, or equivalently, aiming to maximize arbitrary gain functions. We study several properties of pointwise maximal leakage, e.g., how it composes over multiple outcomes, how it is affected by pre- and post-processing, etc. Furthermore, we propose to view privacy leakage as a random variable which, in turn, allows us to regard privacy guarantees as requirements imposed on different statistical properties of the privacy leakage random variable. We define several privacy guarantees and study how they behave under pre-processing, post-processing and composition. Finally, we examine the relationship between pointwise maximal leakage and other privacy notions such as local differential privacy, local information privacy, $f$-information, and so on.