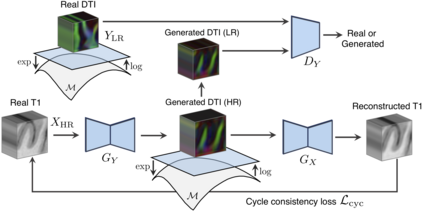
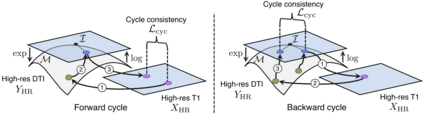
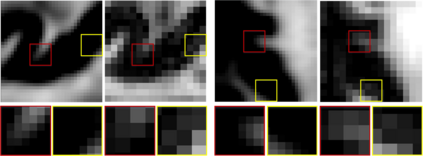
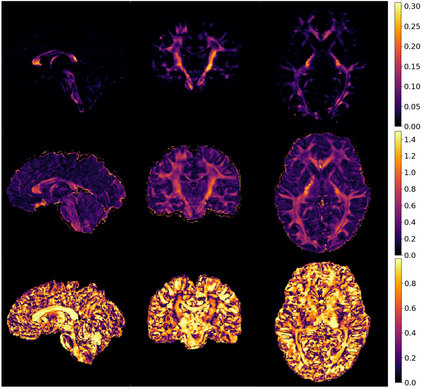
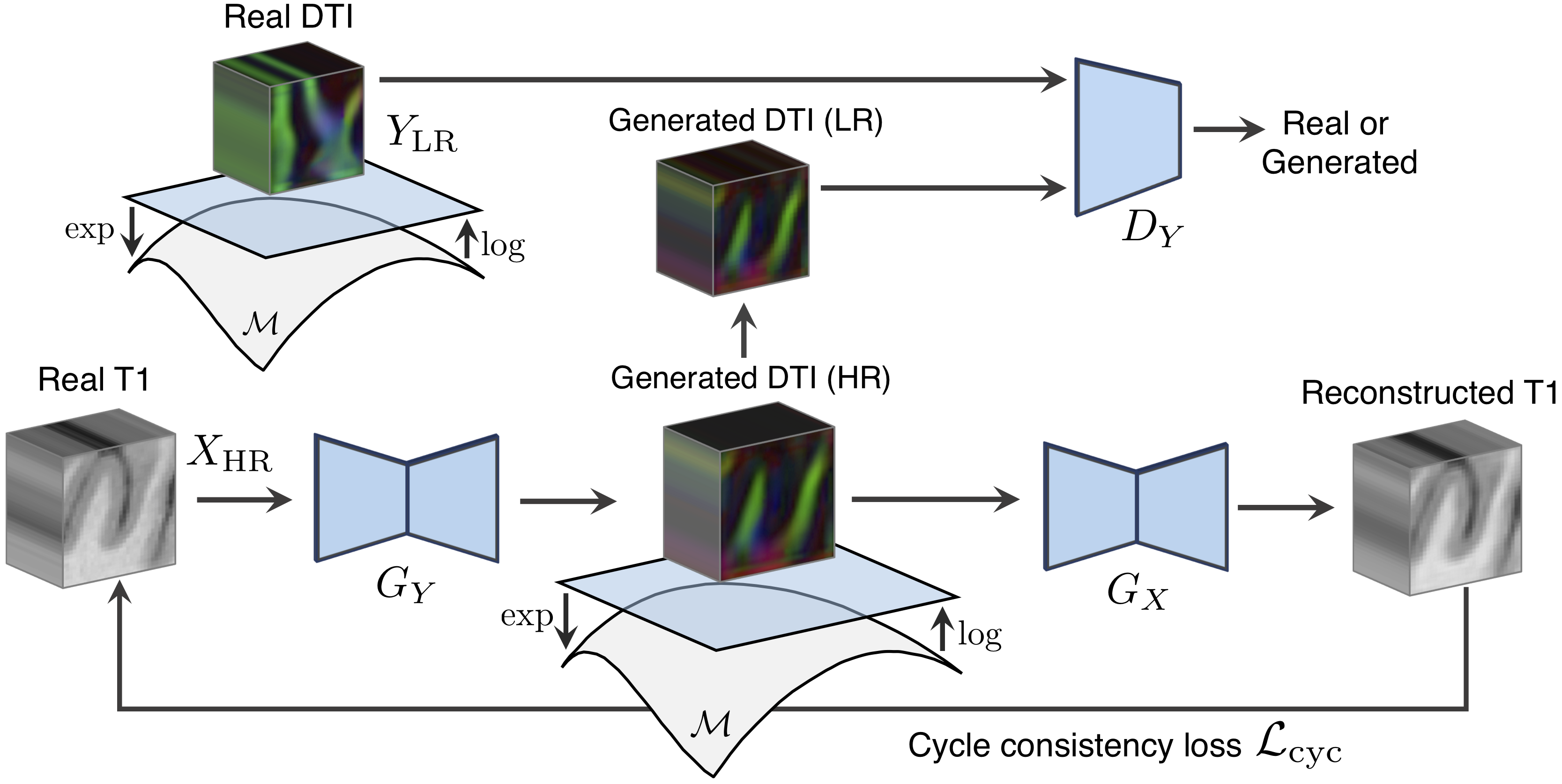
Unpaired image-to-image translation has been applied successfully to natural images but has received very little attention for manifold-valued data such as in diffusion tensor imaging (DTI). The non-Euclidean nature of DTI prevents current generative adversarial networks (GANs) from generating plausible images and has mainly limited their application to diffusion MRI scalar maps, such as fractional anisotropy (FA) or mean diffusivity (MD). Even if these scalar maps are clinically useful, they mostly ignore fiber orientations and therefore have limited applications for analyzing brain fibers. Here, we propose a manifold-aware CycleGAN that learns the generation of high-resolution DTI from unpaired T1w images. We formulate the objective as a Wasserstein distance minimization problem of data distributions on a Riemannian manifold of symmetric positive definite 3x3 matrices SPD(3), using adversarial and cycle-consistency losses. To ensure that the generated diffusion tensors lie on the SPD(3) manifold, we exploit the theoretical properties of the exponential and logarithm maps of the Log-Euclidean metric. We demonstrate that, unlike standard GANs, our method is able to generate realistic high-resolution DTI that can be used to compute diffusion-based metrics and potentially run fiber tractography algorithms. To evaluate our model's performance, we compute the cosine similarity between the generated tensors principal orientation and their ground-truth orientation, the mean squared error (MSE) of their derived FA values and the Log-Euclidean distance between the tensors. We demonstrate that our method produces 2.5 times better FA MSE than a standard CycleGAN and up to 30% better cosine similarity than a manifold-aware Wasserstein GAN while synthesizing sharp high-resolution DTI.
翻译:在自然图像中成功应用了未映射图像到映像的翻译,但对于多值数据,如扩散高压成像(DTI),却很少受到重视。DTI的非欧洲语言性质使得当前基因对抗网络(GANs)无法产生可信的图像,主要将其应用限于传播MRI 标语图,如分数反向图(FA)或中度反射图(MD)。即使这些标语图在临床上有用,它们大多忽略了纤维方向,因此在分析脑纤维方面应用有限。在这里,我们提议了一个多度向导方向GUcliideGAAN,从未映射的T1w图像中学习高分辨率DTI(GANs)的生成。我们把目标设计成瓦瑟斯坦距离最小化数据分布在Riemann的方程式上,例如分数正数3x3矩阵SDD(3),使用以直径直径直的模型和周期一致度损失。为了确保生成的散度变速变速器在SPD(3) 多重,我们利用了主序和直径直径流流流的轨道流流流流的轨道流流的轨流流流流流流流的轨流流流流的轨数据,我们用直径解的轨方法,我们展示的模型和直径解的数学和直径解的轨算的轨算算法的轨算的轨算法的轨算法,我们用了30-直径解法的轨算法。