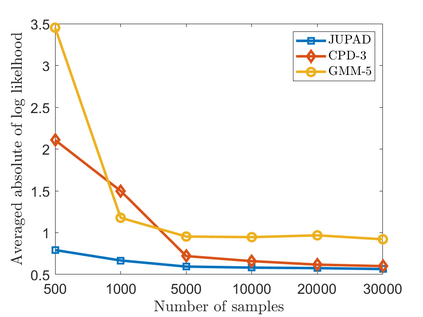
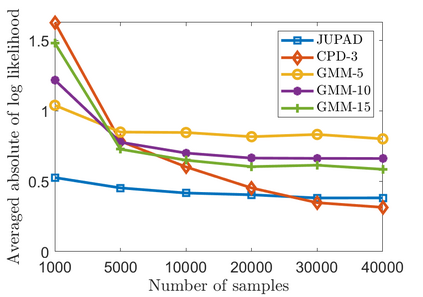
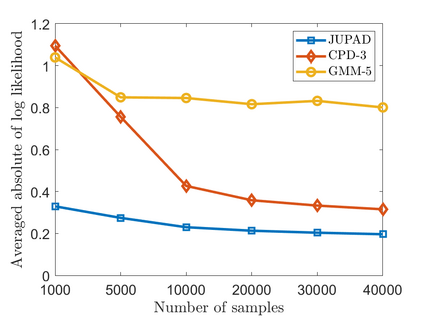
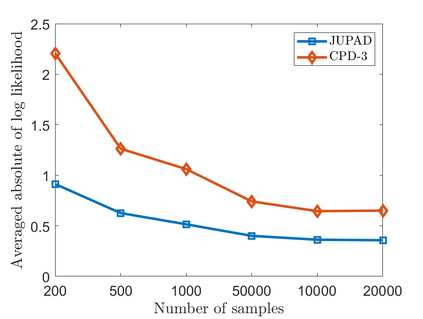
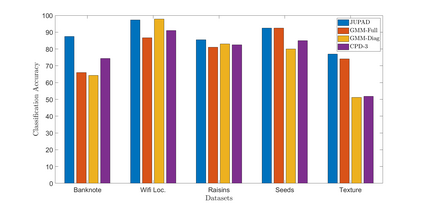
In this work, we study non-parametric estimation of joint probabilities of a given set of discrete and continuous random variables from their (empirically estimated) 2D marginals, under the assumption that the joint probability could be decomposed and approximated by a mixture of product densities/mass functions. The problem of estimating the joint probability density function (PDF) using semi-parametric techniques such as Gaussian Mixture Models (GMMs) is widely studied. However such techniques yield poor results when the underlying densities are mixtures of various other families of distributions such as Laplacian or generalized Gaussian, uniform, Cauchy, etc. Further, GMMs are not the best choice to estimate joint distributions which are hybrid in nature, i.e., some random variables are discrete while others are continuous. We present a novel approach for estimating the PDF using ideas from dictionary representations in signal processing coupled with low rank tensor decompositions. To the best our knowledge, this is the first work on estimating joint PDFs employing dictionaries alongside tensor decompositions. We create a dictionary of various families of distributions by inspecting the data, and use it to approximate each decomposed factor of the product in the mixture. Our approach can naturally handle hybrid $N$-dimensional distributions. We test our approach on a variety of synthetic and real datasets to demonstrate its effectiveness in terms of better classification rates and lower error rates, when compared to state of the art estimators.
翻译:在这项工作中,我们研究了对特定一组离散和连续随机变量的共同概率的不参数估计,这些变量来自其(随机估计)2D边缘,假设联合概率可能分解,并且由产品密度/质量功能的混合作用来估计。使用高萨混合模型等半参数技术来估计联合概率函数(PDF)的问题得到了广泛研究。然而,当基础密度是诸如拉普拉西亚或通用高标、制服、Cauchy等各种其他分布组群的混合物时,这种技术产生的结果很差。此外,GMMM并不是最佳的选择,以估计联合分布的混合性,即某些随机变量是离散的,而另一些则是连续的。我们提出了一个新颖的方法来估计PDF,在信号处理时使用字典表达的理念,同时使用低级的温度-氮分解法。我们最了解的是,这是首次对联合组合组合进行估算,在沙洛尔比或通用高压值条件下使用较低值的词典,在每组中,我们用各种数据序列中,我们用不同的数据序列进行对比分析,我们用不同的方法进行。