A time dependent singularly perturbed problem with shift in space

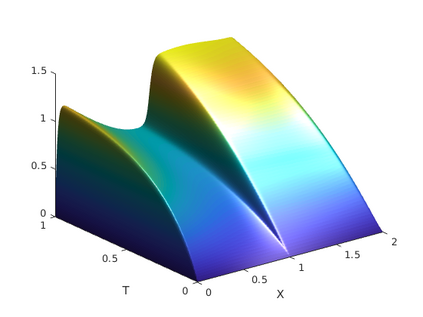
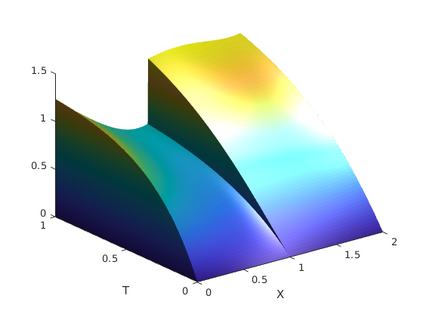
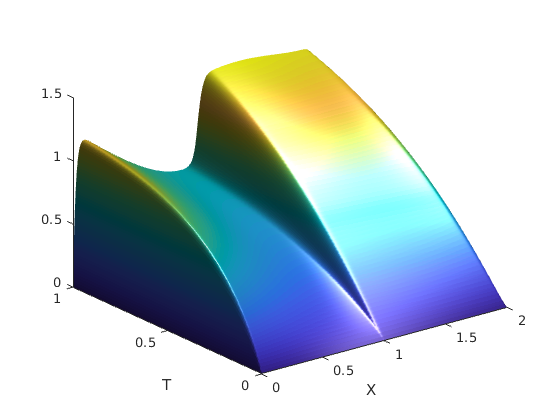
We consider a singularly perturbed time dependent problem with a shift term in space. On appropriately defined layer adapted meshes of Dur\'an- and S-type we derive a-priori error estimates for the stationary problem. Using a discontinuous Galerkin method in time we obtain error estimates for the full discretisation. Introduction of a weighted scalar products and norms allows us to estimate the time-dependent problem in energy and balanced norm. So far it was open to prove such a result. Some numerical results are given to confirm the predicted theory and to show the effect of shifts on the solution.