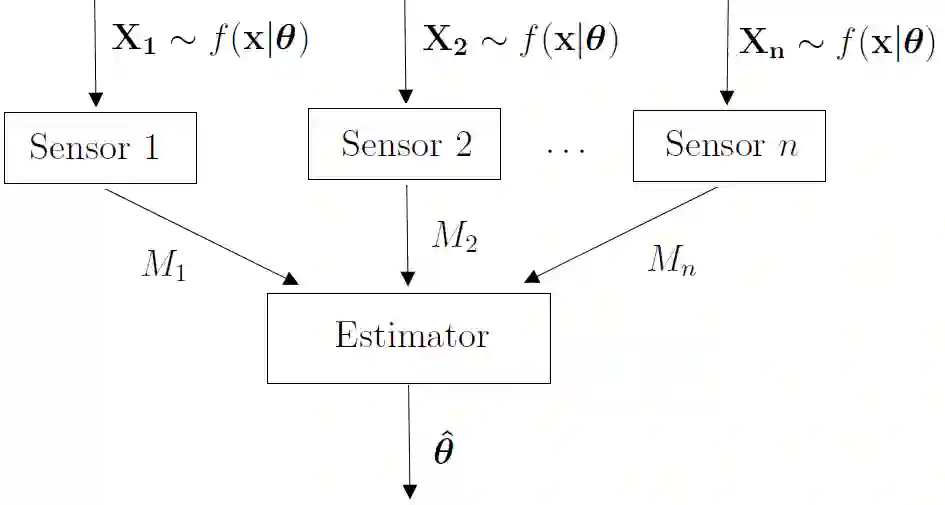
We consider the problem of learning parametric distributions from their quantized samples in a network. Specifically, $n$ agents or sensors observe independent samples of an unknown parametric distribution; and each of them uses $k$ bits to describe its observed sample to a central processor whose goal is to estimate the unknown distribution. First, we establish a generalization of the well-known van Trees inequality to general $L_p$-norms, with $p > 1$, in terms of Generalized Fisher information. Then, we develop minimax lower bounds on the estimation error for two losses: general $L_p$-norms and the related Wasserstein loss from optimal transport.
翻译:我们考虑从网络中的量化样本中学习参数分布的问题。 具体地说, 美元代理商或传感器观察的是未知参数分布的独立样本; 每一个代理商或传感器都使用千元比特向中心处理商描述其观察到的样本, 中心处理商的目标是估计未知分布。 首先, 我们根据一般化的渔业信息,将众所周知的范树的不平等程度概括为一般的1美元/p$-norms, 以1美元/美元/美元/美元/美元/美元/美元/美元/美元/美元/美元/美元/美元/美元/美元/美元/美元/美元/美元/美元/美元/美元/美元/美元/美元/美元/美元/美元/美元/美元/美元/美元/美元/美元/美元/美元/美元/美元/美元/美元/美元/美元/美元/美元/ 10美元/美元/ 10美元/美元/美元/美元/美元/美元/美元/美元/美元/美元/美元/美元/美元/美元/美元/美元/美元/美元/美元/美元/美元/美元/美元/美元/美元/美元/美元/美元/美元/美元/美元/美元/美元/美元/美元/美元/美元/美元/美元/美元/美元/美元/美元/美元/美元/美元/美元/美元/美元/美元/美元/美元/美元/美元/美元/美元/美元/美元/美元/美元/美元/美元/美元/美元/美元/美元/美元/美元/美元/美元/美元/美元/美元/美元/美元/美元/美元/美元/美元/美元/美元/美元/美元/美元/美元/美元/美元/美元/美元/美元/美元/美元/美元/美元/美元/美元/美元/美元/美元/美元/美元/美元/美元/美元/美元/美元/美元/美元/美元/美元/美元/美元/美元/美元/美元/美元/美元/美元/美元/美元/美元/美元/美元/美元/美元/美元/美元/美元/美元/美元/美元/美元/美元/美元/美元/美元/美元/美元/美元/美元/美元/美元/美元/美元/美元/美元/美元/美元/美元/美元/美元/美元/美元/美元/美元/美元/美元/美元/