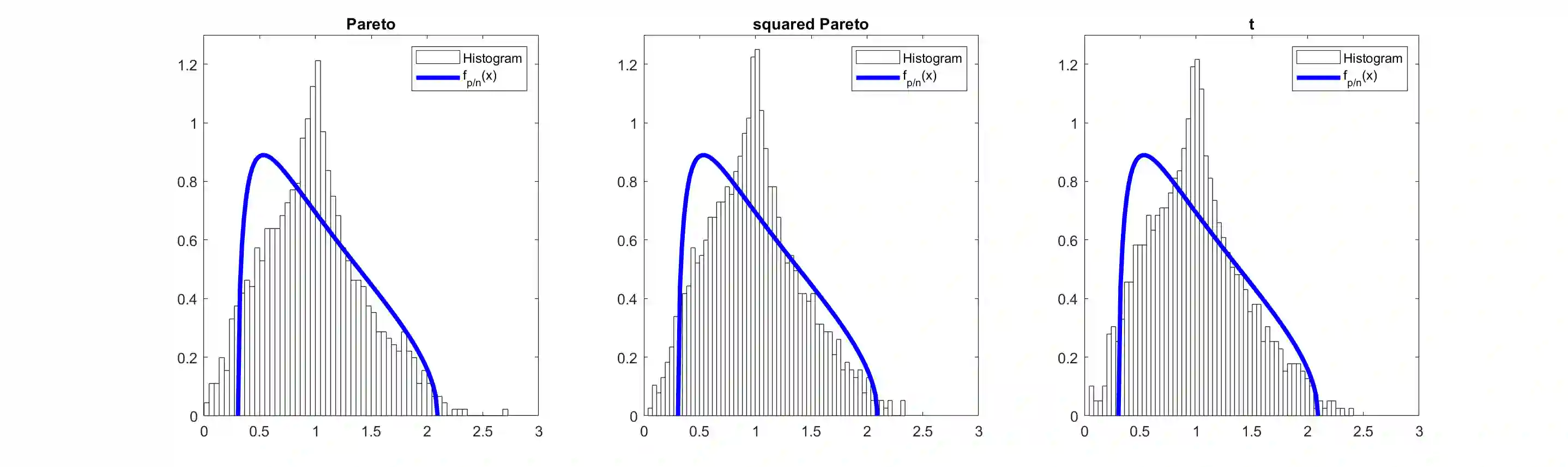
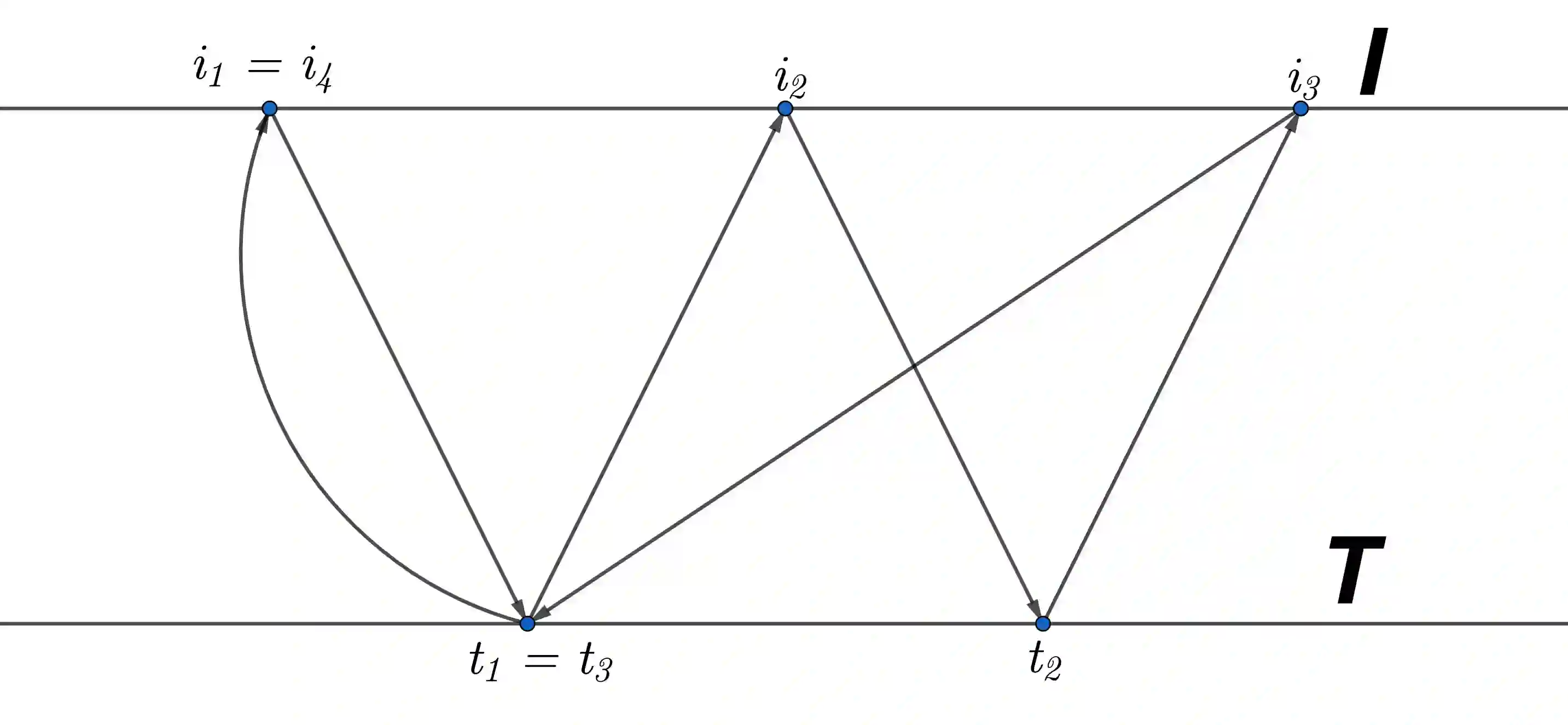
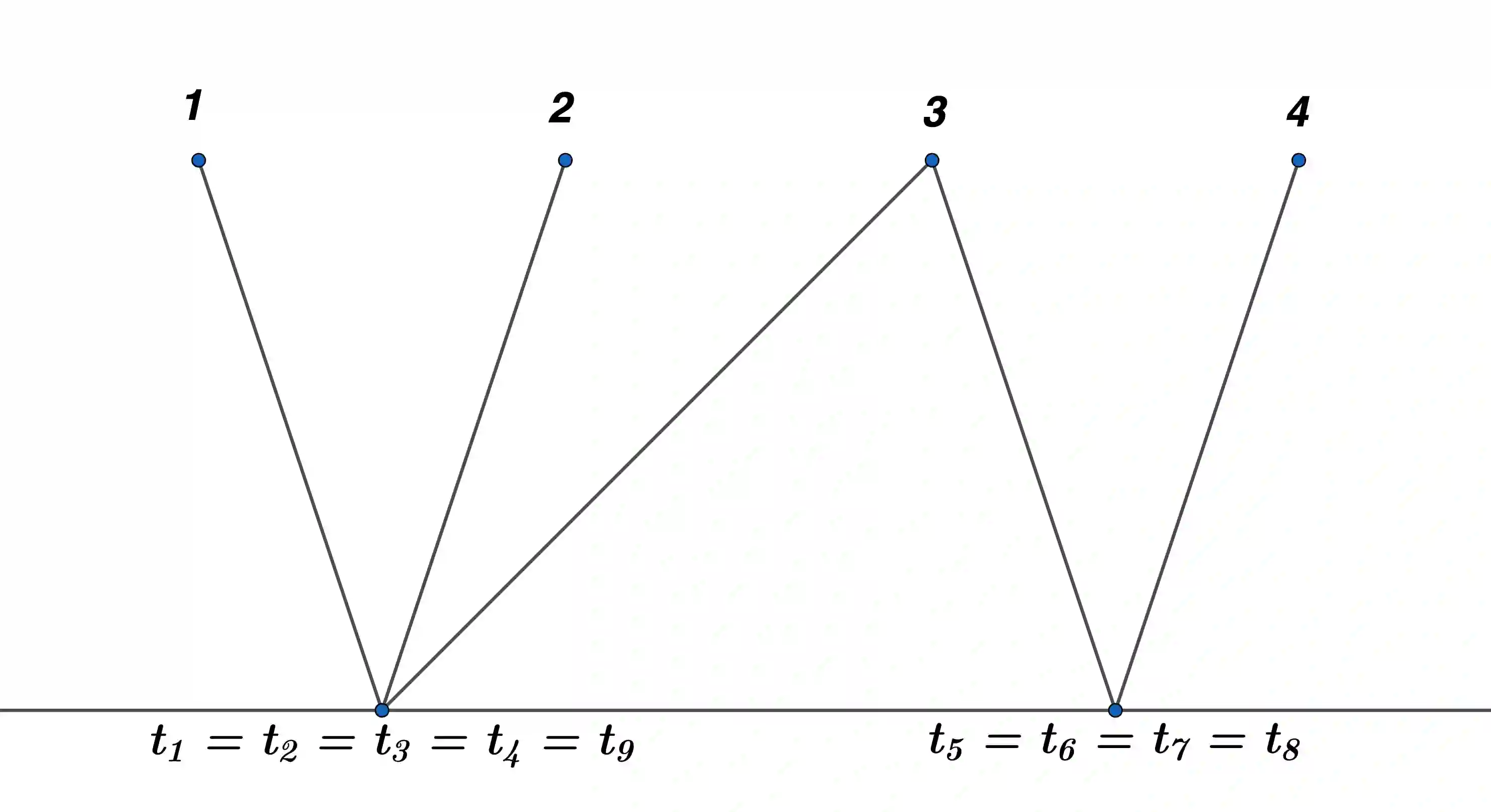
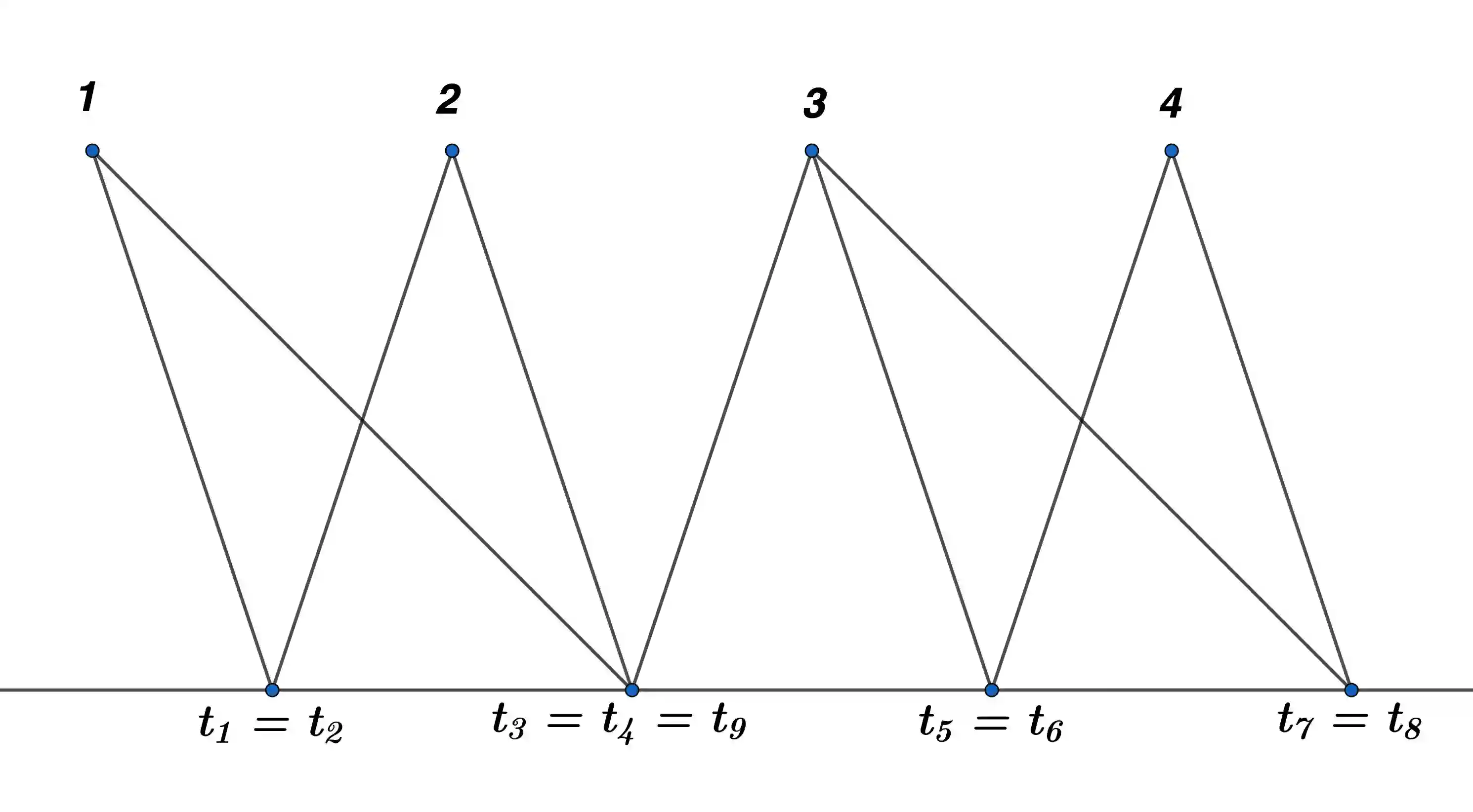
Consider a $p$-dimensional population ${\mathbf x} \in\mathbb{R}^p$ with iid coordinates in the domain of attraction of a stable distribution with index $\alpha\in (0,2)$. Since the variance of ${\mathbf x}$ is infinite, the sample covariance matrix ${\mathbf S}_n=n^{-1}\sum_{i=1}^n {{\mathbf x}_i}{\mathbf x}'_i$ based on a sample ${\mathbf x}_1,\ldots,{\mathbf x}_n$ from the population is not well behaved and it is of interest to use instead the sample correlation matrix ${\mathbf R}_n= \{\operatorname{diag}({\mathbf S}_n)\}^{-1/2}\, {\mathbf S}_n \{\operatorname{diag}({\mathbf S}_n)\}^{-1/2}$. This paper finds the limiting distributions of the eigenvalues of ${\mathbf R}_n$ when both the dimension $p$ and the sample size $n$ grow to infinity such that $p/n\to \gamma \in (0,\infty)$. The family of limiting distributions $\{H_{\alpha,\gamma}\}$ is new and depends on the two parameters $\alpha$ and $\gamma$. The moments of $H_{\alpha,\gamma}$ are fully identified as sum of two contributions: the first from the classical Mar\v{c}enko-Pastur law and a second due to heavy tails. Moreover, the family $\{H_{\alpha,\gamma}\}$ has continuous extensions at the boundaries $\alpha=2$ and $\alpha=0$ leading to the Mar\v{c}enko-Pastur law and a modified Poisson distribution, respectively. Our proofs use the method of moments, the path-shortening algorithm developed in [18] and some novel graph counting combinatorics. As a consequence, the moments of $H_{\alpha,\gamma}$ are expressed in terms of combinatorial objects such as Stirling numbers of the second kind. A simulation study on these limiting distributions $H_{\alpha,\gamma}$ is also provided for comparison with the Mar\v{c}enko-Pastur law.
翻译:考虑一个 $ $ mathbf x} = $ mathbf = 美元 = mathbf = = $ mathb = = = $ mathb = $ mathb = $ = mathbf = $ = mathbf x = = mathb= = mathb= = mathb = = = $ = mathb = = 美元 = mathb = = mathb = = max = max = = ocx = max = = max = = max = = = = $ $ = = max = max = = max = = max = = max = = = = max = = = max = = = = max = = = = max = = = = = = = = = = = = = = = = max = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =