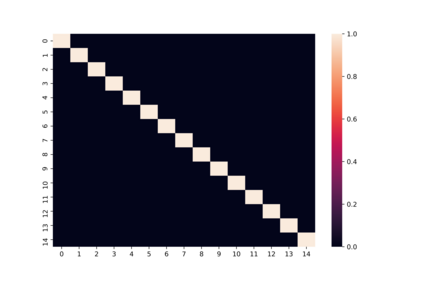
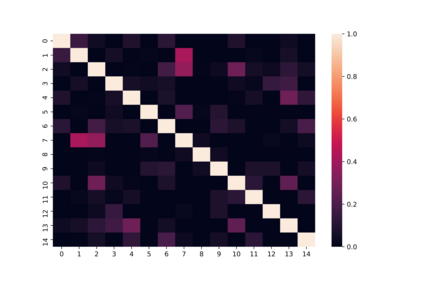
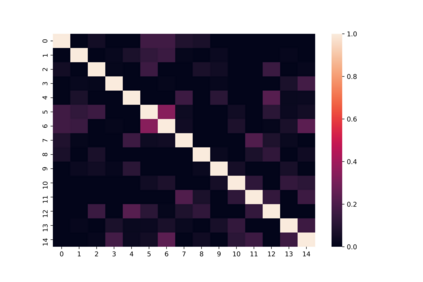
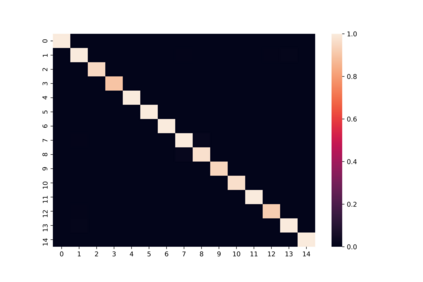
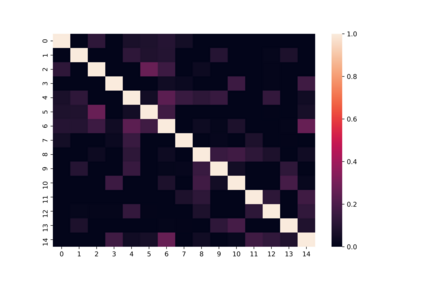
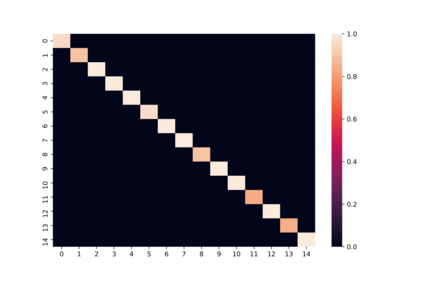
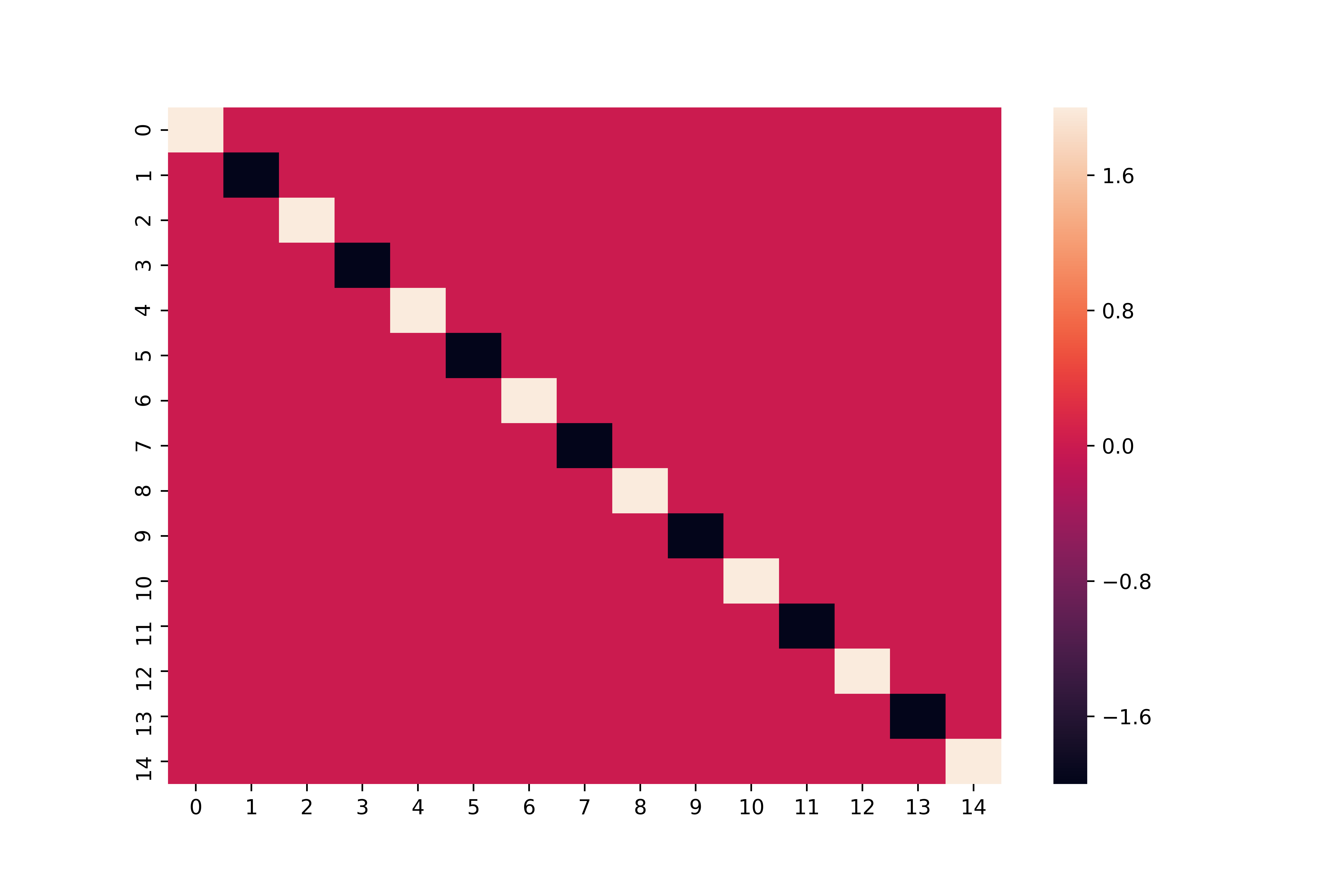
Harvey et al. (2010) extended the Bayesian estimation method by Sahu et al. (2003) to a multivariate skew-elliptical distribution with a general skewness matrix, and applied it to Bayesian portfolio optimization with higher moments. Although their method is epochal in the sense that it can handle the skewness dependency among asset returns and incorporate higher moments into portfolio optimization, it cannot identify all elements in the skewness matrix due to label switching in the Gibbs sampler. To deal with this identification issue, we propose to modify their sampling algorithm by imposing a positive lower-triangular constraint on the skewness matrix of the multivariate skew- elliptical distribution and improved interpretability. Furthermore, we propose a Bayesian sparse estimation of the skewness matrix with the horseshoe prior to further improve the accuracy. In the simulation study, we demonstrate that the proposed method with the identification constraint can successfully estimate the true structure of the skewness dependency while the existing method suffers from the identification issue.
翻译:Harvey等人(2010年)将Sahu等人(2003年)的Bayesian估计方法扩展为多变式的Skew-lipstical分布法,采用一般的Skiwness 矩阵,并将其应用于Bayesian组合优化法,在高时段对Bayesian组合进行优化。虽然这种方法很时髦,因为它能够处理资产回报中的斜度依赖性,并将更高时段纳入组合优化,但无法查明由于Gibbs采样器中标签转换而导致的斜度矩阵中的所有要素。为了处理这一识别问题,我们提议修改其抽样算法,对多变式 skew-lipptical分布的偏重度矩阵施加积极的低度角限制,并提高可解释性。此外,我们提议对Bayesian对马蹄之前的斜度矩阵进行稀疏度估计,以进一步提高准确性。在模拟研究中,我们证明,带有识别制约性的拟议方法能够成功地估计斜度依赖性的真正结构,而现有方法则存在识别问题。