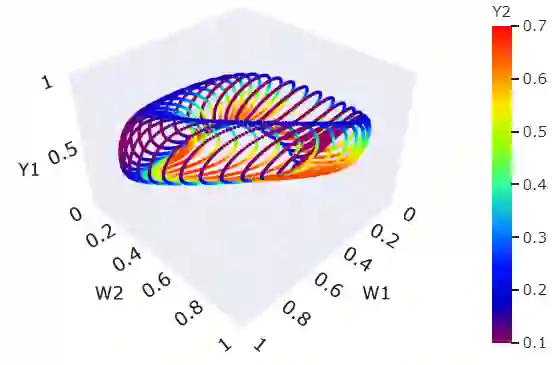
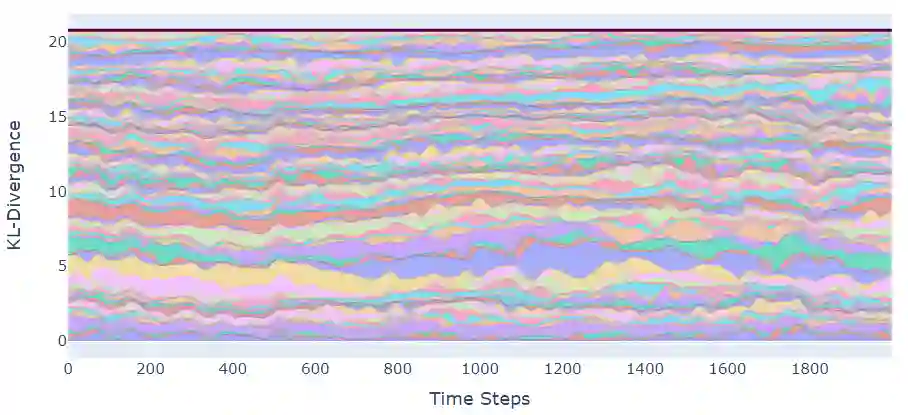
The predominant paradigm in evolutionary game theory and more generally online learning in games is based on a clear distinction between a population of dynamic agents that interact given a fixed, static game. In this paper, we move away from the artificial divide between dynamic agents and static games, to introduce and analyze a large class of competitive settings where both the agents and the games they play evolve strategically over time. We focus on arguably the most archetypal game-theoretic setting -- zero-sum games (as well as network generalizations) -- and the most studied evolutionary learning dynamic -- replicator, the continuous-time analogue of multiplicative weights. Populations of agents compete against each other in a zero-sum competition that itself evolves adversarially to the current population mixture. Remarkably, despite the chaotic coevolution of agents and games, we prove that the system exhibits a number of regularities. First, the system has conservation laws of an information-theoretic flavor that couple the behavior of all agents and games. Secondly, the system is Poincar\'{e} recurrent, with effectively all possible initializations of agents and games lying on recurrent orbits that come arbitrarily close to their initial conditions infinitely often. Thirdly, the time-average agent behavior and utility converge to the Nash equilibrium values of the time-average game. Finally, we provide a polynomial time algorithm to efficiently predict this time-average behavior for any such coevolving network game.
翻译:进化游戏理论以及更普遍的游戏中在线学习的主导范式是基于一种明确的区分,即:在固定的、静态的游戏中互动的动态代理人的人群之间有明显区别。在本文中,我们摆脱了动态代理人与静态游戏之间的人为鸿沟,引入并分析一大批竞争环境,在这些环境中,他们玩的代理人和游戏都随着时间的演变而演变。我们关注的是最古老的游戏理论环境 -- -- 零和游戏(以及网络的概括化) -- -- 以及最受研究的进化学习动态 -- -- 复制者,倍增重量的连续时间类比。在零和竞争中,代理人和游戏的人群相互竞争,而这种零和游戏本身与当前人口混合的对立。值得注意的是,尽管代理人和游戏的演变是混乱的,我们证明这个系统表现出了一定的规律性。首先,这个系统保存着一种将所有代理人和游戏行为和游戏的行为结合起来的信息-理论调味的规律。第二,这个系统是反复出现,所有可能的代理人和游戏的初始模拟。 游戏的开始和游戏游戏游戏游戏的游戏的游戏的游戏周期性,最终的稳定性,我们可以任意地接近到一个稳定的游戏的游戏的游戏的游戏的周期性, 。这个游戏的游戏的游戏的游戏的周期性,我们最终的游戏的游戏的游戏的游戏的周期性, 提供了一个无限的游戏的游戏的游戏的游戏的周期性, 的周期性, 我们的游戏的游戏的周期性, 的游戏的游戏的游戏的游戏的游戏的周期性,最终的周期性, 的周期性, 的周期性,我们的周期性, 的周期性,我们的游戏的周期性, 我们的游戏的游戏的游戏的周期性, 我们的周期性, 的周期性, 我们的游戏的周期性, 的游戏的周期性, 的周期性,我们的游戏的游戏的游戏的周期性, 的周期性,我们的周期性, 的周期性, 的游戏的游戏的游戏的游戏的周期性,我们的周期性, 的周期性, 的周期性,我们的游戏的游戏的周期性, 的周期性,我们的游戏的周期性, 我们的周期性, 的周期性,我们的周期性, 的周期性