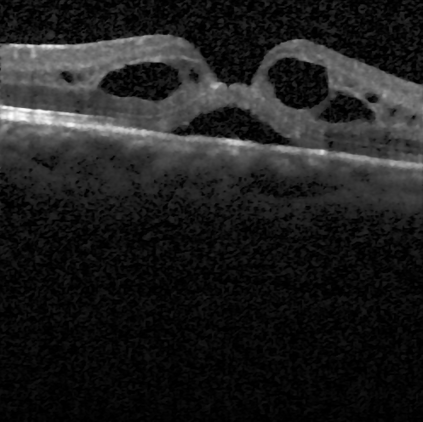
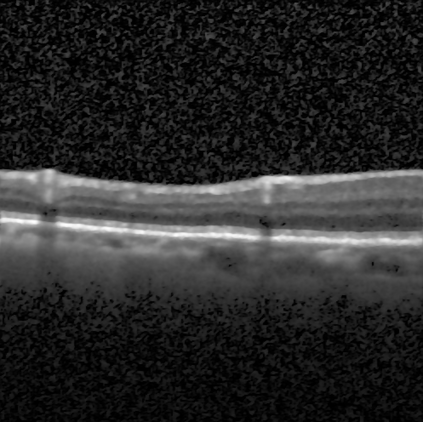
The Euler Elastica (EE) model with surface curvature can generate artifact-free results compared with the traditional total variation regularization model in image processing. However, strong nonlinearity and singularity due to the curvature term in the EE model pose a great challenge for one to design fast and stable algorithms for the EE model. In this paper, we propose a new, fast, hybrid alternating minimization (HALM) algorithm for the EE model based on a bilinear decomposition of the gradient of the underlying image and prove the global convergence of the minimizing sequence generated by the algorithm under mild conditions. The HALM algorithm comprises three sub-minimization problems and each is either solved in the closed form or approximated by fast solvers making the new algorithm highly accurate and efficient. We also discuss the extension of the HALM strategy to deal with general curvature-based variational models, especially with a Lipschitz smooth functional of the curvature. A host of numerical experiments are conducted to show that the new algorithm produces good results with much-improved efficiency compared to other state-of-the-art algorithms for the EE model. As one of the benchmarks, we show that the average running time of the HALM algorithm is at most one-quarter of that of the fast operator-splitting-based Deng-Glowinski-Tai algorithm.
翻译:暂无翻译