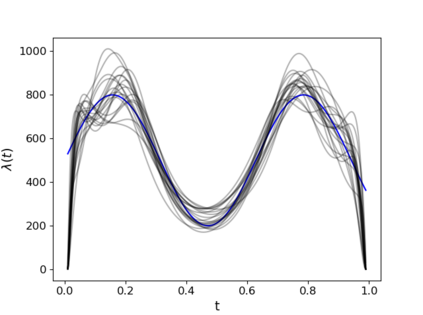
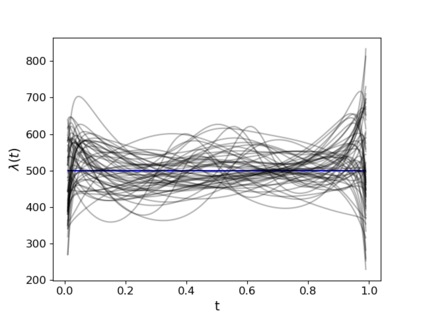
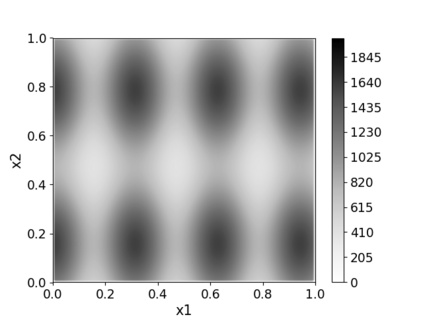
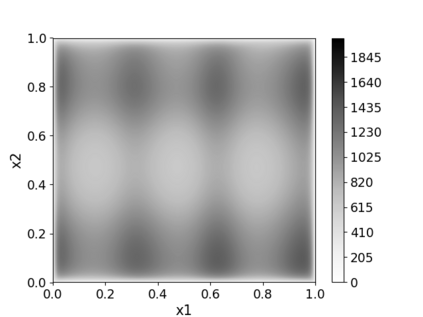
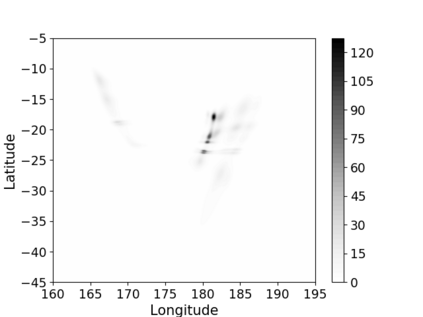
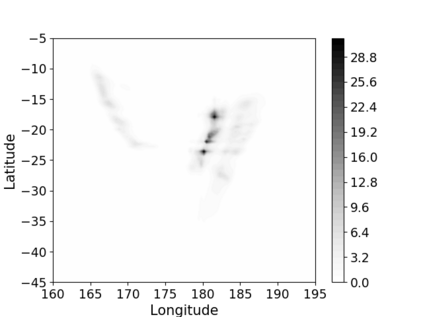
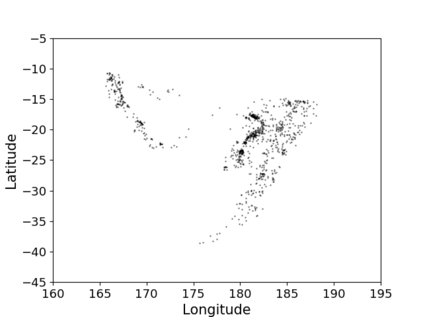
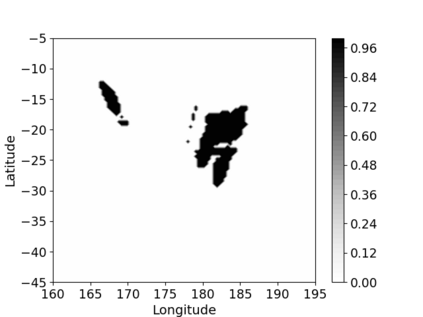
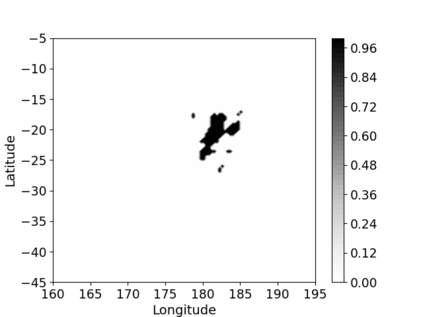
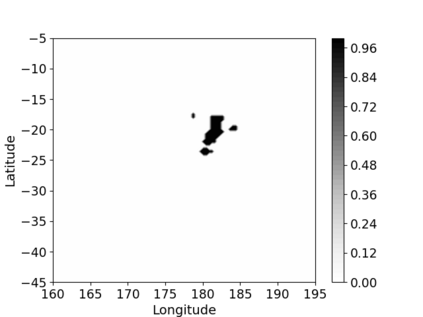
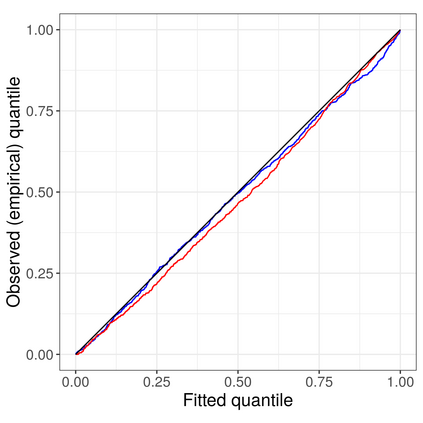
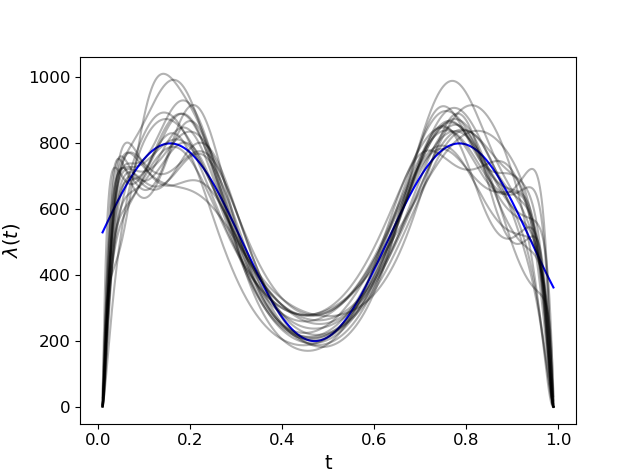
Non-Homogeneous Poisson Process Intensity Modeling and Estimation using Measure Transport

Non-homogeneous Poisson processes are used in a wide range of scientific disciplines, ranging from the environmental sciences to the health sciences. Often, the central object of interest in a point process is the underlying intensity function. Here, we present a general model for the intensity function of a non-homogeneous Poisson process using measure transport. The model is built from a flexible bijective mapping that maps from the underlying intensity function of interest to a simpler reference intensity function. We enforce bijectivity by modeling the map as a composition of multiple simple bijective maps, and show that the model exhibits an important approximation property. Estimation of the flexible mapping is accomplished within an optimization framework, wherein computations are efficiently done using recent technological advances in deep learning and a graphics processing unit. Although we find that intensity function estimates obtained with our method are not necessarily superior to those obtained using conventional methods, the modeling representation brings with it other advantages such as facilitated point process simulation and uncertainty quantification. Modeling point processes in higher dimensions is also facilitated using our approach. We illustrate the use of our model on both simulated data, and a real data set containing the locations of seismic events near Fiji since 1964.