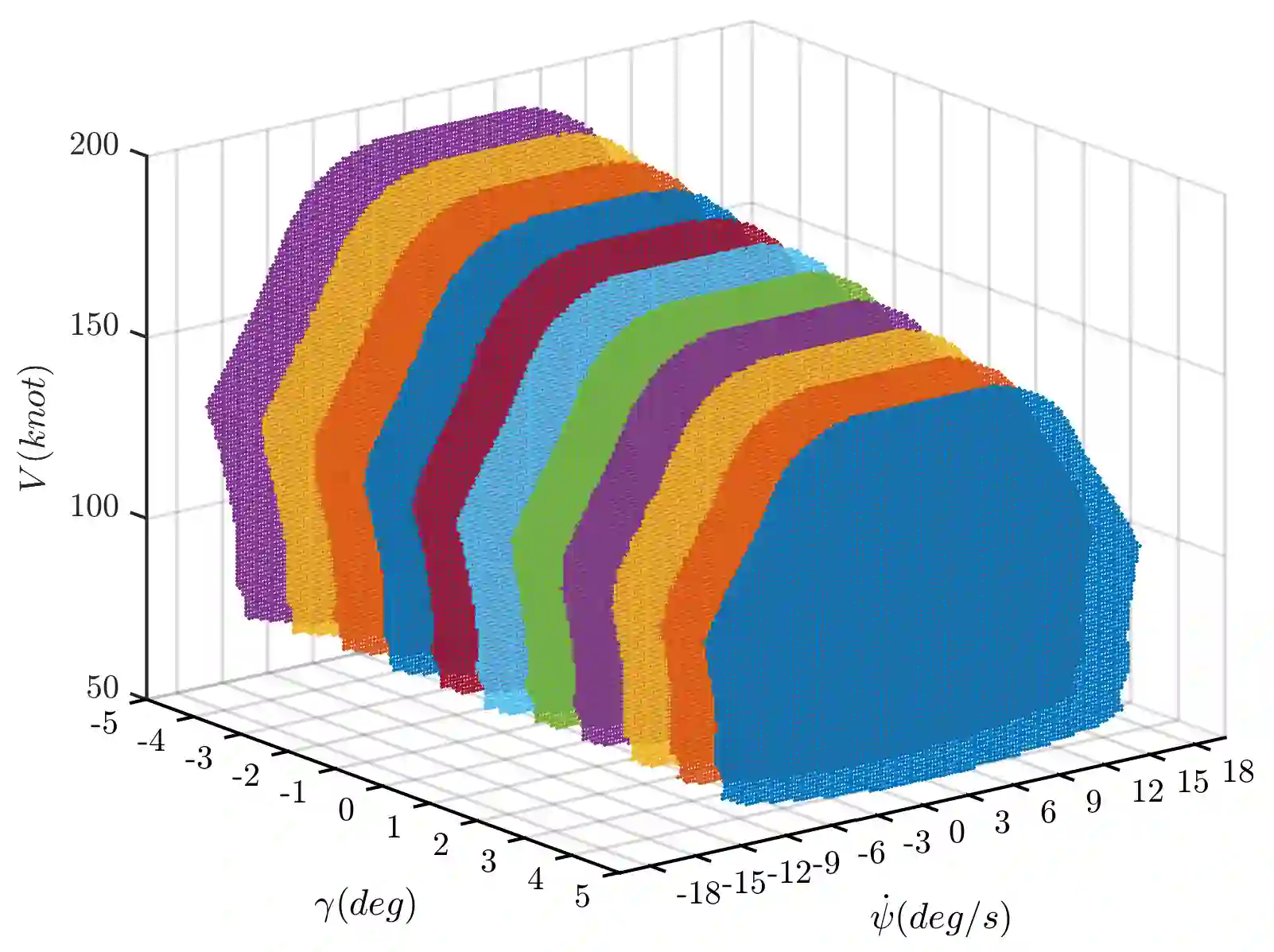
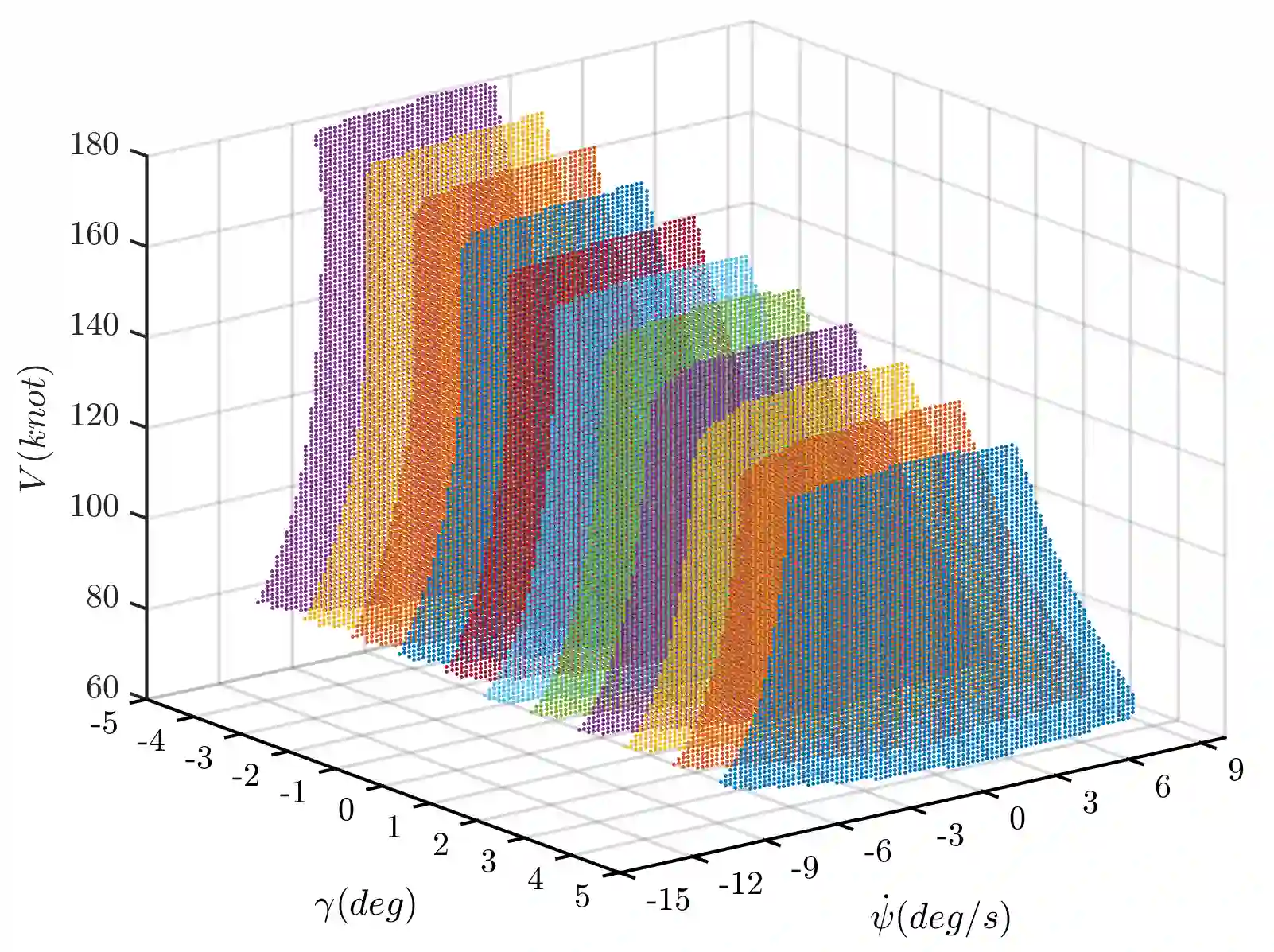
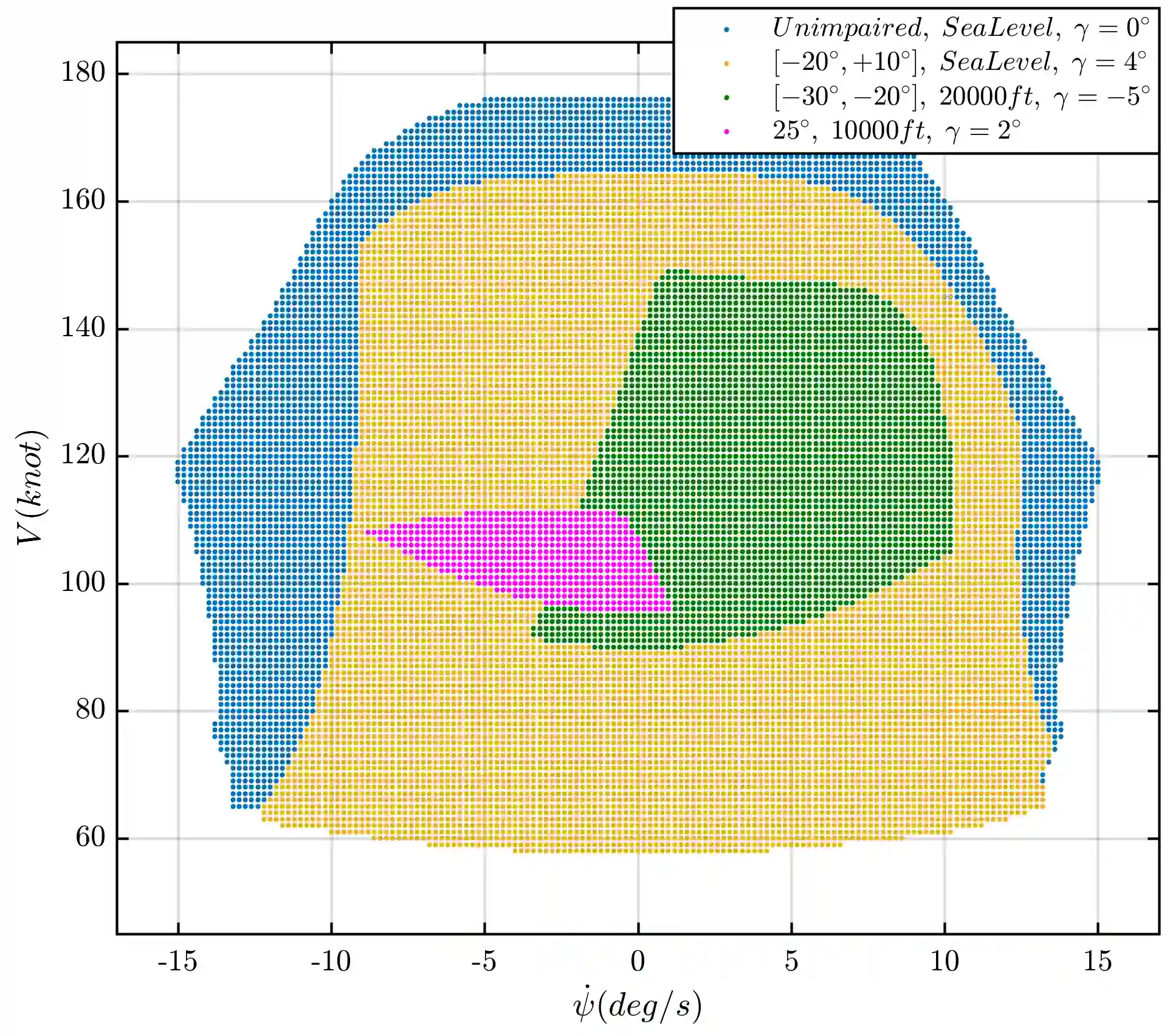
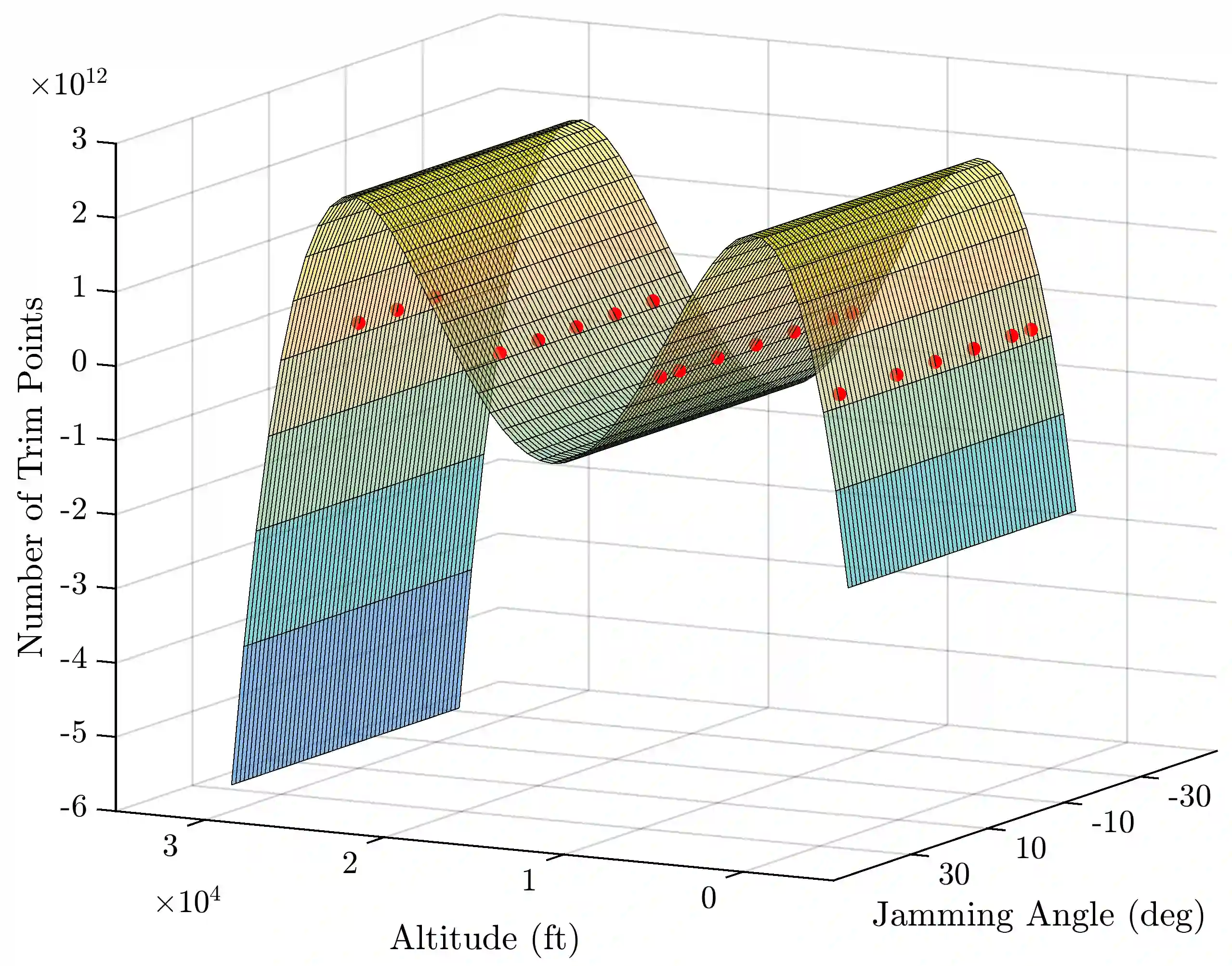
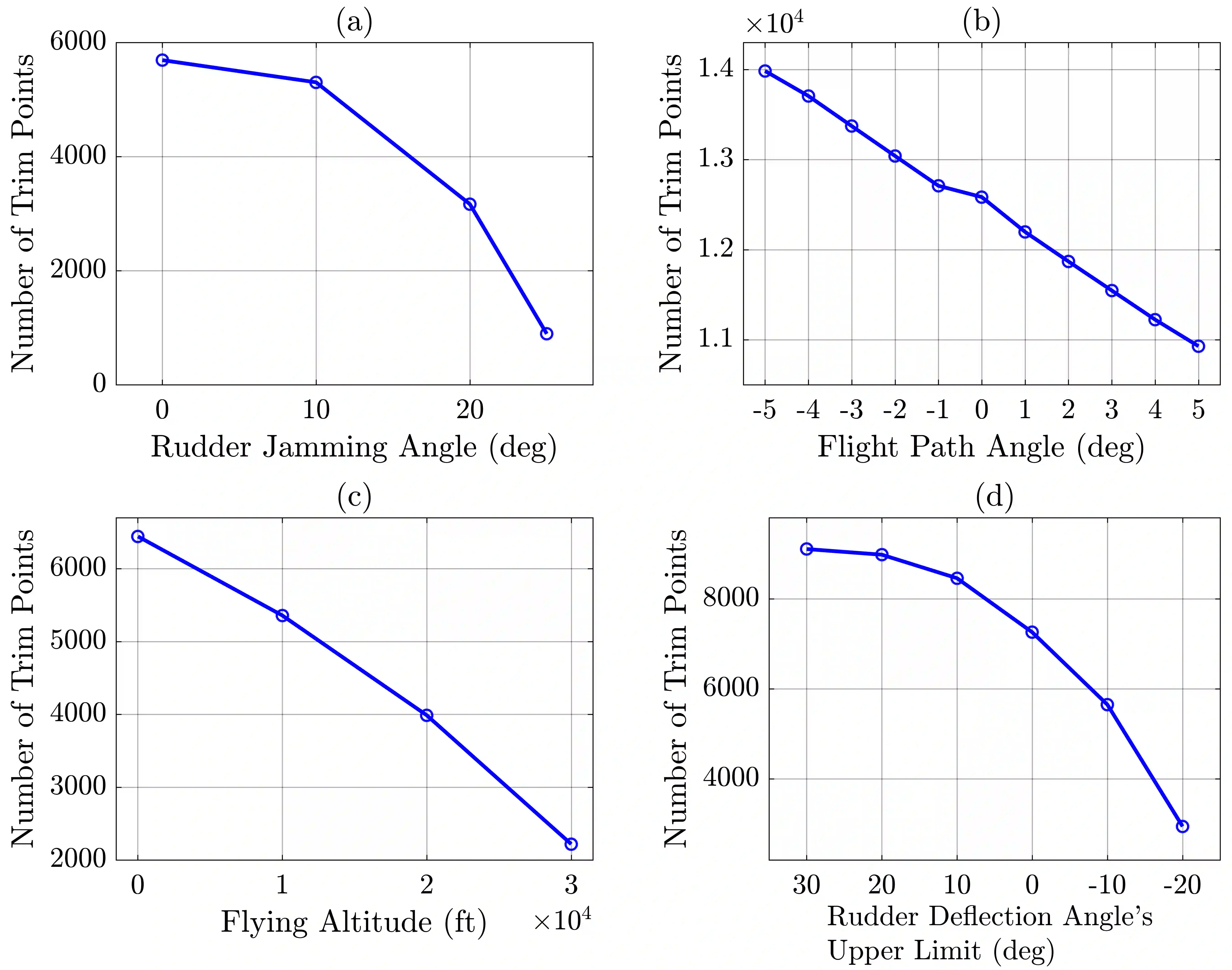
Aircraft failures alter the aircraft dynamics and cause maneuvering flight envelope to change. Such envelope variations are nonlinear and generally unpredictable by the pilot as they are governed by the aircraft complex dynamics. Hence, in order to prevent in-flight Loss of Control it is crucial to practically predict the impaired aircraft's flight envelope variation due to any a-priori unknown failure degree. This paper investigates the predictability of the number of trim points within the maneuvering flight envelope and its centroid using both linear and nonlinear least-squares estimation methods. To do so, various polynomial models and nonlinear models based on hyperbolic tangent function are developed and compared which incorporate the influencing factors on the envelope variations as the inputs and estimate the centroid and the number of trim points of the maneuvering flight envelope at any intended failure degree. Results indicate that both the polynomial and hyperbolic tangent function-based models are capable of predicting the impaired fight envelope variation with good precision. Furthermore, it is shown that the regression equation of the best polynomial fit enables direct assessment of the impaired aircraft's flight envelope contraction and displacement sensitivity to the specific parameters characterizing aircraft failure and flight condition.
翻译:飞机失灵会改变飞机的动态,并导致飞行信封变化。这种信封变异是非线性且通常不可预测的,因为飞行员受飞机复杂动态的制约。因此,为了防止在飞行中失去控制,对于实际预测由于任何优先未知失灵程度而受损的飞机的飞行信封变异至关重要。本文用线性和非线性最低平方估计方法,调查操纵飞行信封及其中机器人内三角点数的可预测性。为了这样做,将开发出各种多球模型和基于超斜对照功能的非线性模型,并进行比较,其中纳入信封变的影响因素,作为输入量和估计的机器人,以及在任何预期失灵程度调整飞行信封的三点数目。结果显示,以多球和高叶色函数为基础的模型都能够以精确度预测受损的战斗信封变异。此外,还表明,最佳多球型模型的回归方格能够直接评估受损的飞机的飞行信封收缩和偏差对具体参数的飞行失灵和飞行状态的敏感度。