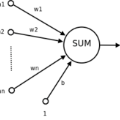
To gain a deeper understanding of the behavior and learning dynamics of (deep) artificial neural networks, it is valuable to employ mathematical abstractions and models. These tools provide a simplified perspective on network performance and facilitate systematic investigations through simulations. In this paper, we propose utilizing the framework of stochastic processes, which has been underutilized thus far. Our approach models activation patterns of thresholded nodes in (deep) artificial neural networks as stochastic processes. We focus solely on activation frequency, leveraging neuroscience techniques used for real neuron spike trains. During a classification task, we extract spiking activity and use an arrival process following the Poisson distribution. We examine observed data from various artificial neural networks in image recognition tasks, fitting the proposed model's assumptions. Through this, we derive parameters describing activation patterns in each network. Our analysis covers randomly initialized, generalizing, and memorizing networks, revealing consistent differences across architectures and training sets. Calculating Mean Firing Rate, Mean Fano Factor, and Variances, we find stable indicators of memorization during learning, providing valuable insights into network behavior. The proposed model shows promise in describing activation patterns and could serve as a general framework for future investigations. It has potential applications in theoretical simulations, pruning, and transfer learning.
翻译:暂无翻译