Analyzing cross-talk between superimposed signals: Vector norm dependent hidden Markov models and applications

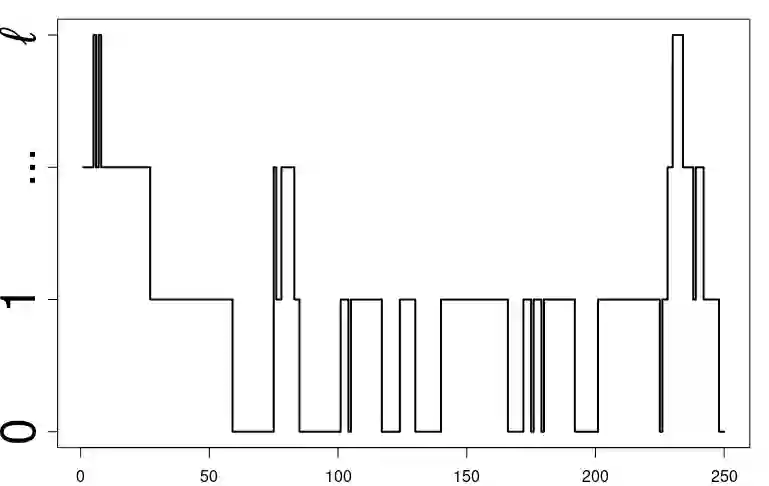
We propose and investigate a hidden Markov model (HMM) for the analysis of aggregated, super-imposed two-state signal recordings. A major motivation for this work is that often these recordings cannot be observed individually but only their superposition. Among others, such models are in high demand for the understanding of cross-talk between ion channels, where each single channel might take two different states which cannot be measured separately. As an essential building block we introduce a parametrized vector norm dependent Markov chain model and characterize it in terms of permutation invariance as well as conditional independence. This leads to a hidden Markov chain "sum" process which can be used for analyzing aggregated two-state signal observations within a HMM. Additionally, we show that the model parameters of the vector norm dependent Markov chain are uniquely determined by the parameters of the "sum" process and are therefore identifiable. Finally, we provide algorithms to estimate the parameters and apply our methodology to real-world ion channel data measurements, where we show competitive gating.