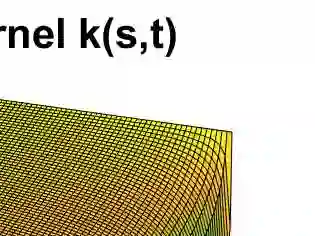
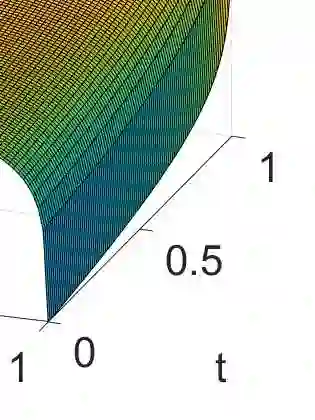
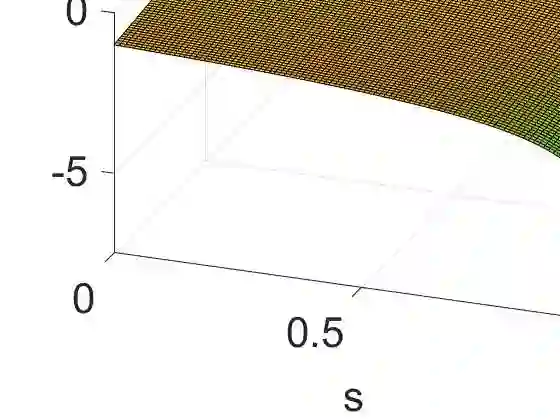
复合线性问题处理不当的程度,重点是非合同Hausdorf瞬时操作员的影响 (The degree of ill-posedness of composite linear ill-posed problems with focus on the impact of the non-compact Hausdorff moment operator)

We consider compact composite linear operators in Hilbert space, where the composition is given by some compact operator followed by some non-compact one possessing a non-closed range. Focus is on the impact of the non-compact factor on the overall behaviour of the decay rates of the singular values of the composition. Specifically, the composition of the compact integration operator with the non-compact Hausdorff moment operator is considered. We show that the singular values of the composition decay faster than the ones of the integration operator, providing a first example of this kind. However, there is a gap between available lower bounds for the decay rate and the obtained result. Therefore we conclude with a discussion.

翻译：我们考虑的是Hilbert空间的紧凑复合线性操作员,其构成由某些紧凑操作员提供,然后由一些非封闭范围的非契约操作员提供。重点是非契约因素对组成单数值衰减率总体行为的影响。具体地说,考虑的是与非复合Hausdorff瞬间操作员的紧凑集成操作员的构成。我们表明,组成单数值的衰减速度比一体化操作员的更快,提供了这方面的第一个例子。然而,现有衰减率下限与所得结果之间存在差距。因此,我们以讨论结束。