A novel relaxation scheme for the numerical approximation of Schrödinger-Poisson type systems

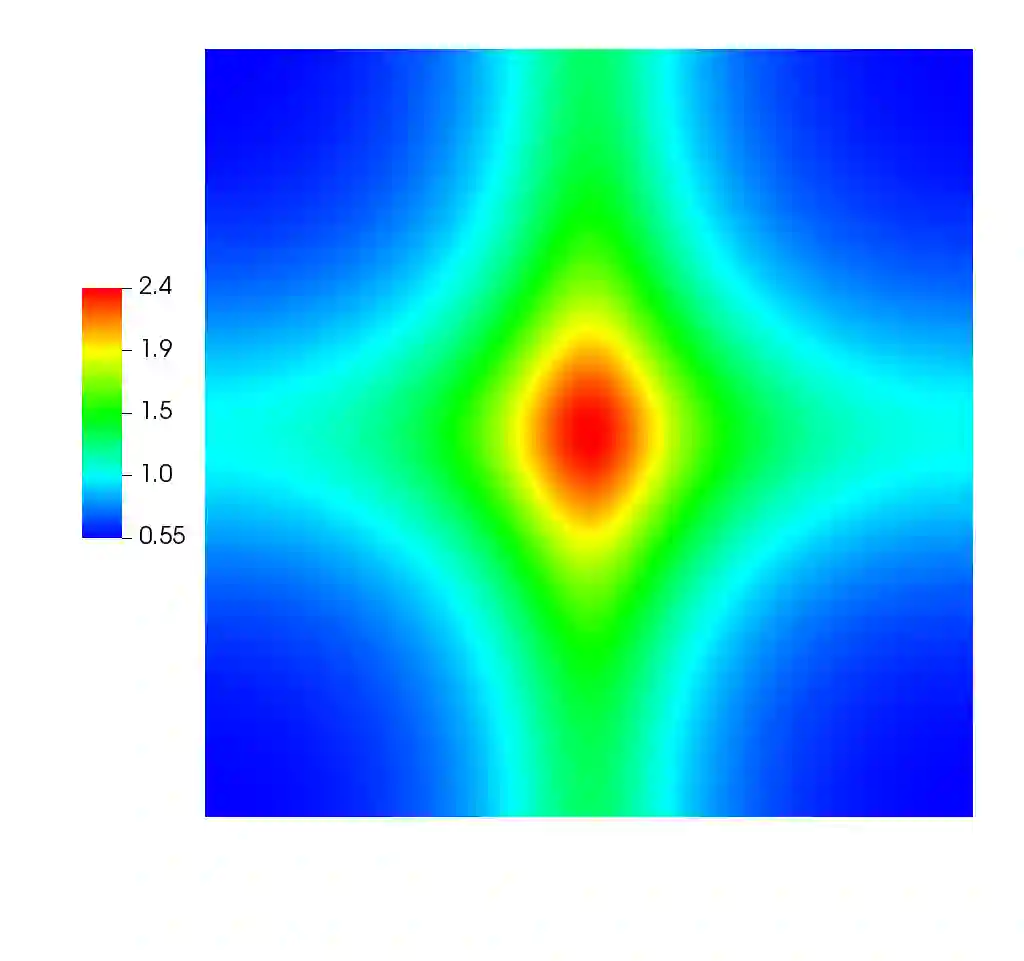
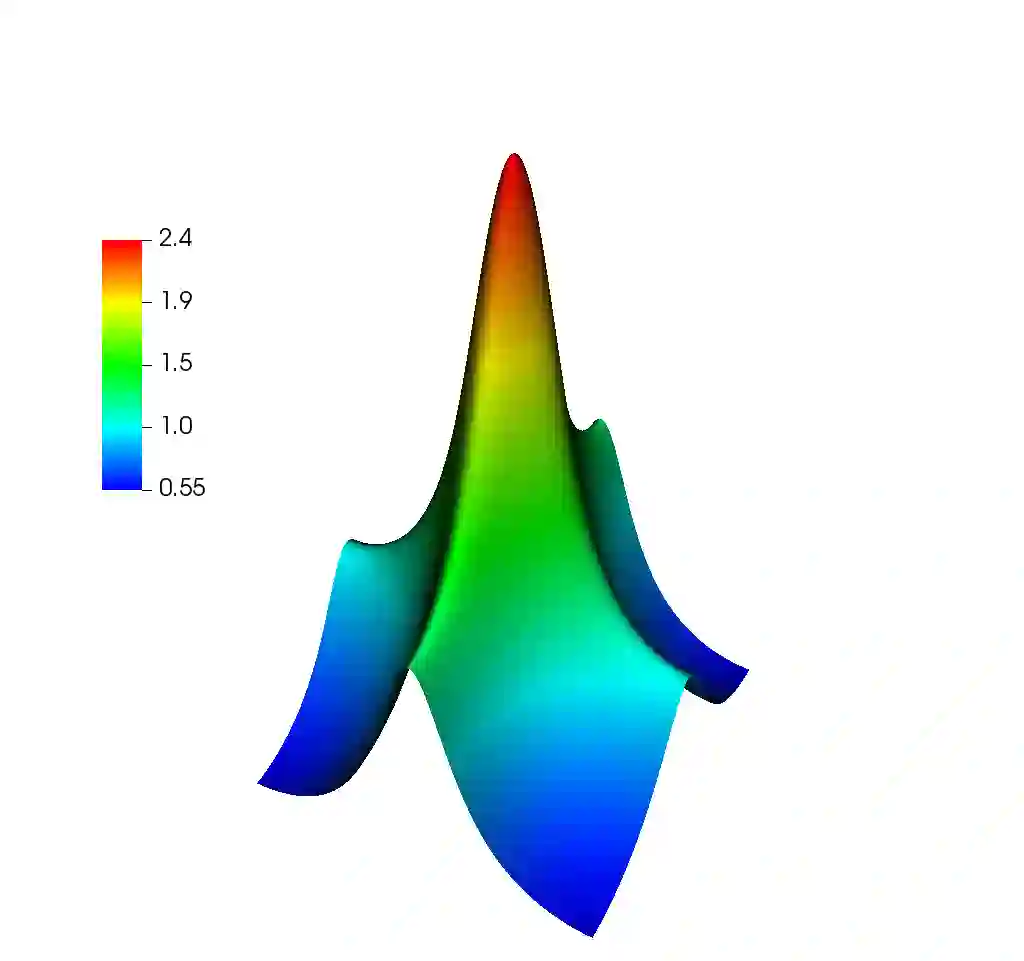
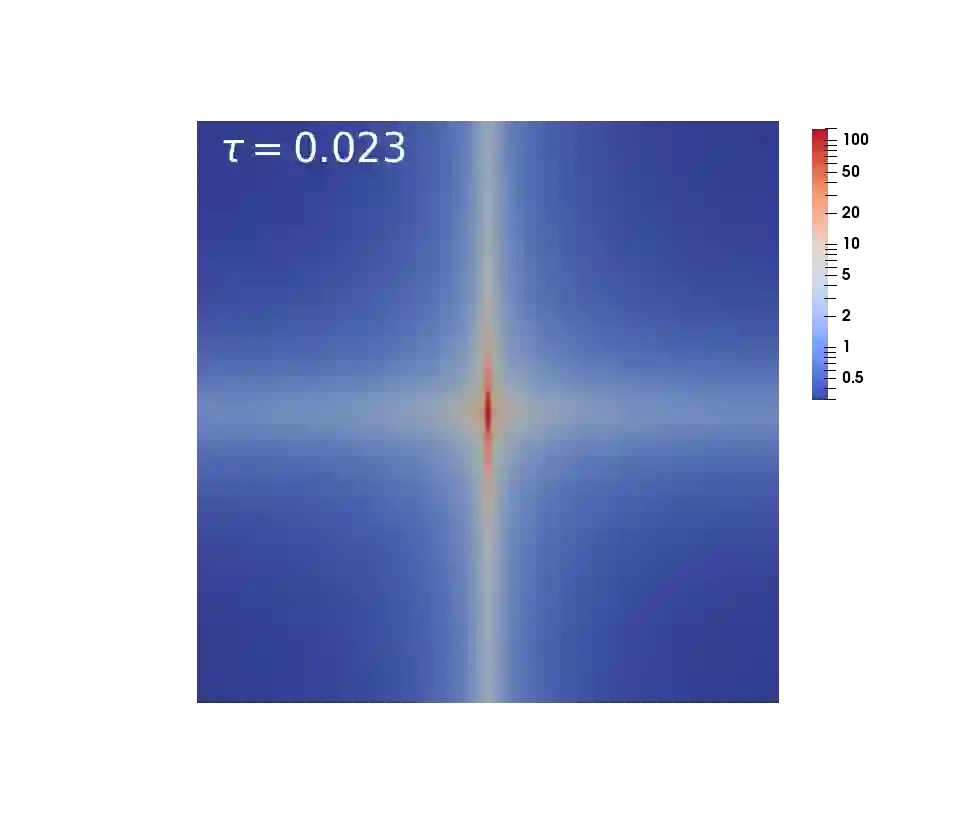
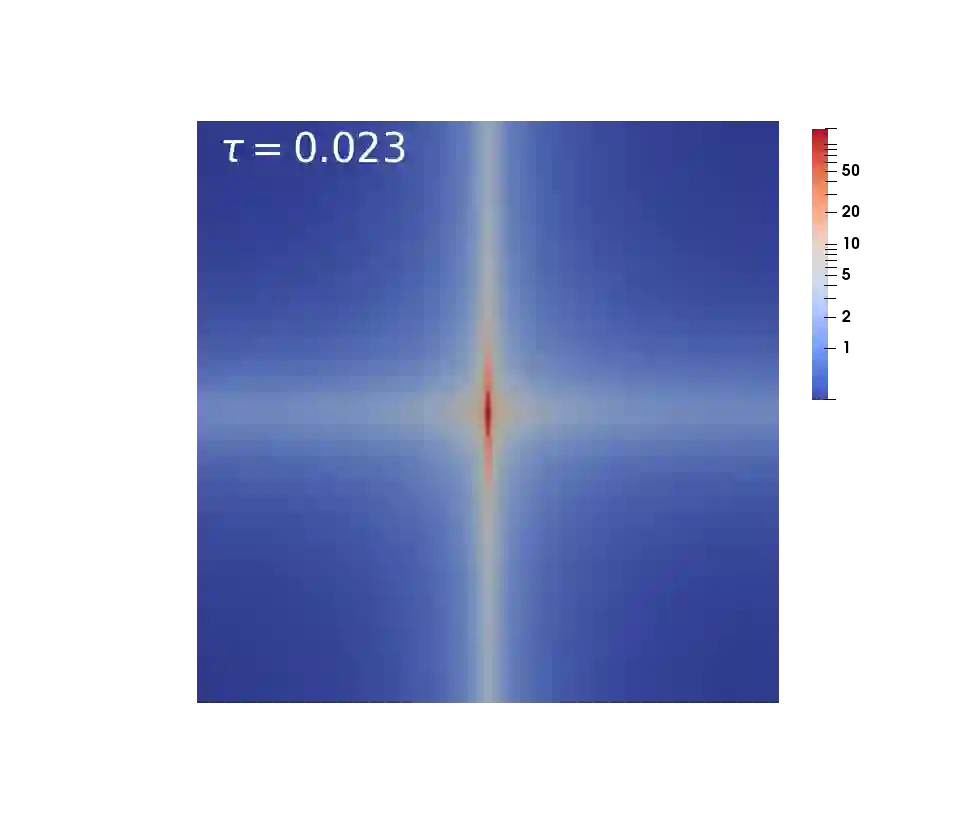
We introduce a new second order in time relaxation-type scheme for approximating solutions of the Schr\"odinger-Poisson system. More specifically, we use the Crank-Nicolson scheme as a time stepping mechanism, whilst the nonlinearity is handled by means of a relaxation approach in the spirit of \cite{Besse, KK} for the nonlinear Schr\"odinger equation. For the spatial discretisation we use the standard conforming finite element scheme. The resulting scheme is explicit with respect to the nonlinearity, satisfies discrete versions of the system's conservation laws, and is seen to be second order in time. We conclude by presenting some numerical experiments, including an example from cosmology, that demonstrate the effectiveness and robustness of the new scheme.