A relaxed-inertial forward-backward-forward algorithm for Stochastic Generalized Nash equilibrium seeking

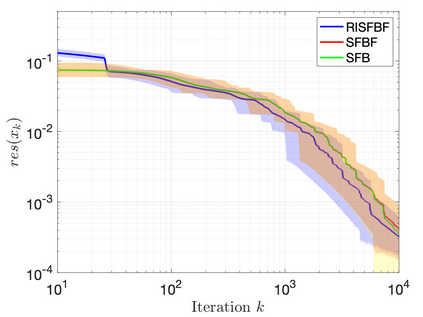
In this paper we propose a new operator splitting algorithm for distributed Nash equilibrium seeking under stochastic uncertainty, featuring relaxation and inertial effects. Our work is inspired by recent deterministic operator splitting methods, designed for solving structured monotone inclusion problems. The algorithm is derived from a forward-backward-forward scheme for solving structured monotone inclusion problems featuring a Lipschitz continuous and monotone game operator. To the best of our knowledge, this is the first distributed (generalized) Nash equilibrium seeking algorithm featuring acceleration techniques in stochastic Nash games without assuming cocoercivity. Numerical examples illustrate the effect of inertia and relaxation on the performance of our proposed algorithm.