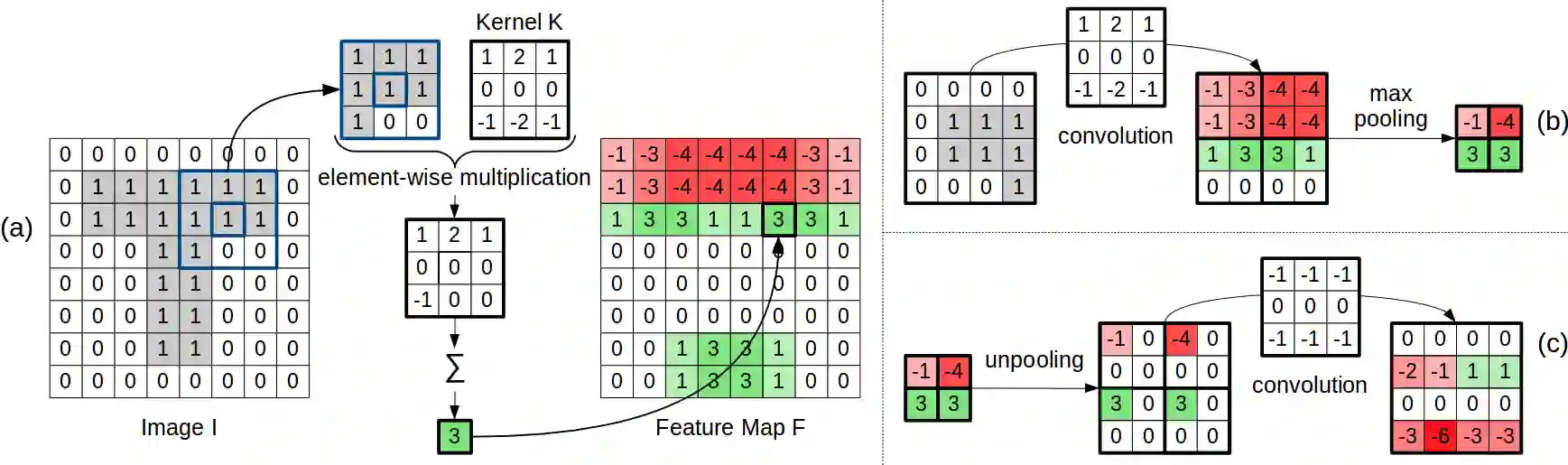
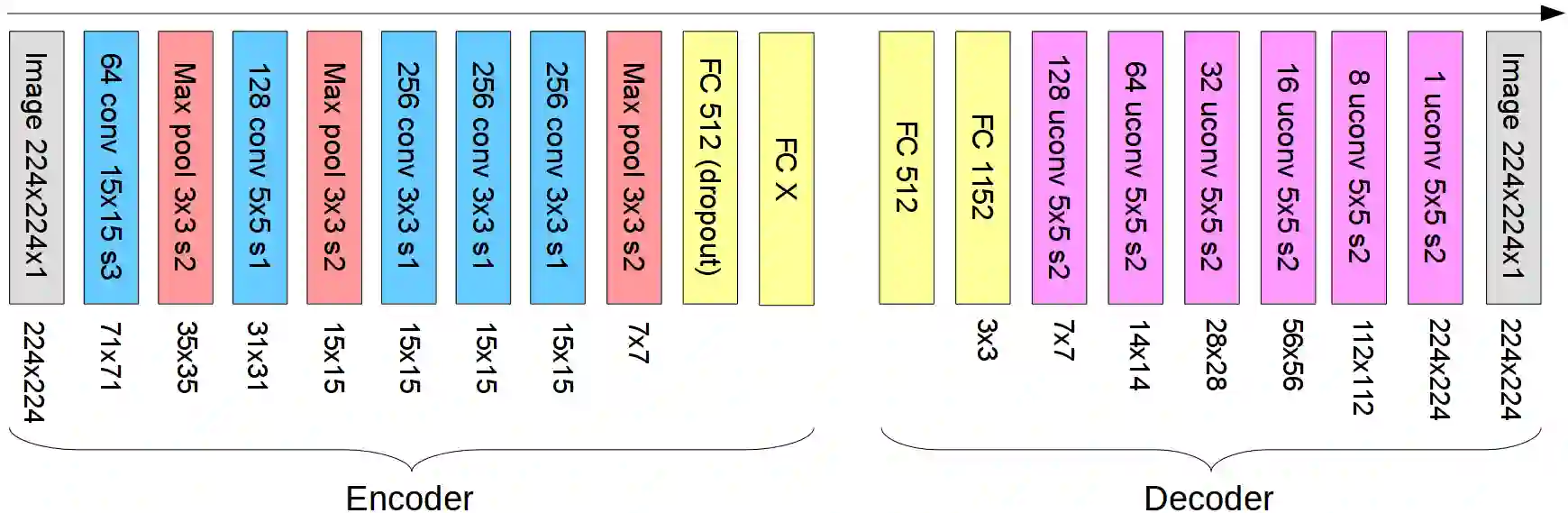
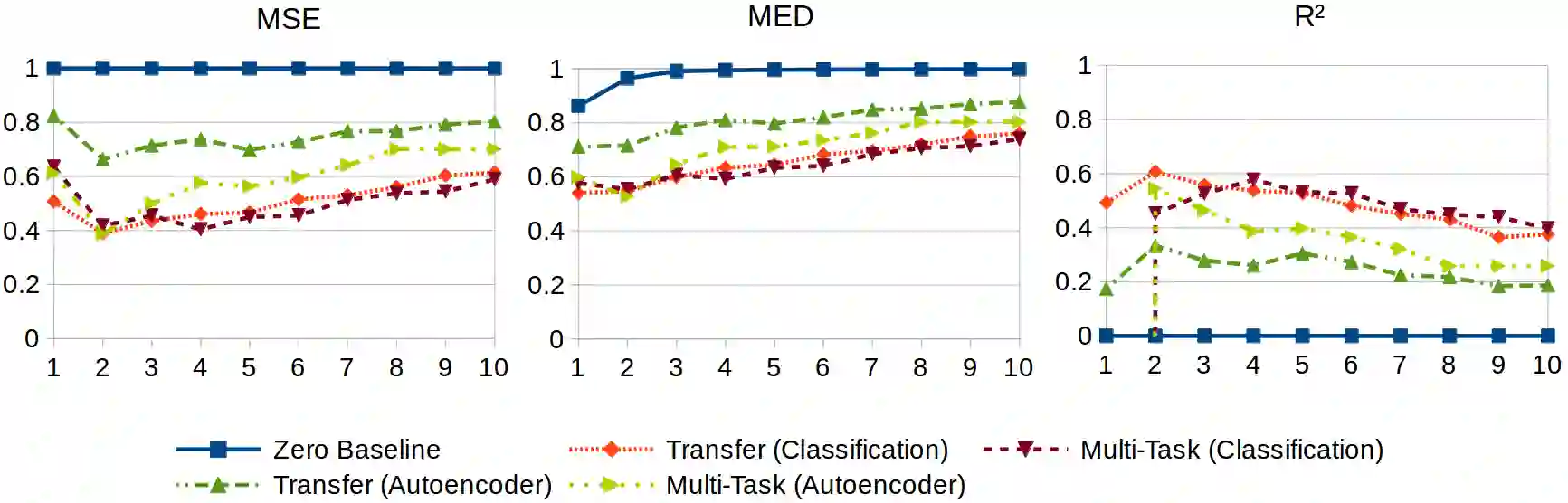
Shape information is crucial for human perception and cognition, and should therefore also play a role in cognitive AI systems. We employ the interdisciplinary framework of conceptual spaces, which proposes a geometric representation of conceptual knowledge through low-dimensional interpretable similarity spaces. These similarity spaces are often based on psychological dissimilarity ratings for a small set of stimuli, which are then transformed into a spatial representation by a technique called multidimensional scaling. Unfortunately, this approach is incapable of generalizing to novel stimuli. In this paper, we use convolutional neural networks to learn a generalizable mapping between perceptual inputs (pixels of grayscale line drawings) and a recently proposed psychological similarity space for the shape domain. We investigate different network architectures (classification network vs. autoencoder) and different training regimes (transfer learning vs. multi-task learning). Our results indicate that a classification-based multi-task learning scenario yields the best results, but that its performance is relatively sensitive to the dimensionality of the similarity space.
翻译:形状信息对人类感知和认知至关重要,因此也应在认知AI系统中发挥作用。我们采用概念空间的跨学科框架,提出通过低维可解释的相似空间对概念知识进行几何表达。这些相似空间往往基于对一小组刺激的心理差异性评级,然后通过一个称为多层面规模的技术将其转换为空间代表。不幸的是,这一方法无法概括为新颖的刺激。在本文中,我们利用进化神经网络学习概念投入(灰度线图像素)和最近提议的形状域心理相似空间之间的通用绘图。我们调查不同的网络结构(分类网络相对于自动编码器)和不同的培训制度(转移学习与多塔克学习)。我们的结果表明,基于分类的多塔克学习情景产生最佳效果,但其性能对相似空间的维度相对敏感。