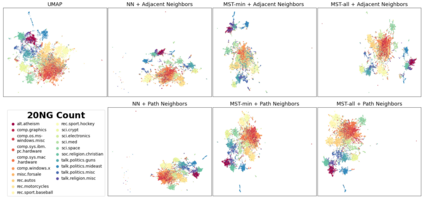
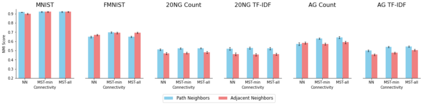
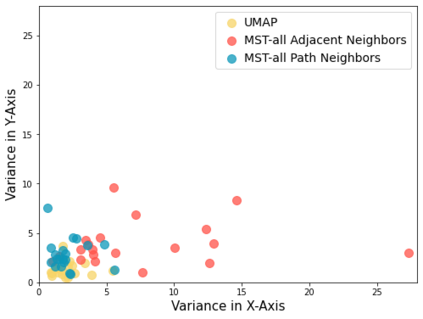
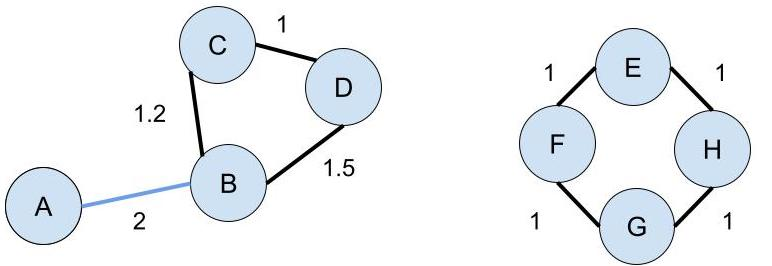
Topology based dimensionality reduction methods such as t-SNE and UMAP have seen increasing success and popularity in high-dimensional data. These methods have strong mathematical foundations and are based on the intuition that the topology in low dimensions should be close to that of high dimensions. Given that the initial topological structure is a precursor to the success of the algorithm, this naturally raises the question: What makes a "good" topological structure for dimensionality reduction? Insight into this will enable us to design better algorithms which take into account both local and global structure. In this paper which focuses on UMAP, we study the effects of node connectivity (k-Nearest Neighbors vs mutual k-Nearest Neighbors) and relative neighborhood (Adjacent via Path Neighbors) on dimensionality reduction. We explore these concepts through extensive ablation studies on 4 standard image and text datasets; MNIST, FMNIST, 20NG, AG, reducing to 2 and 64 dimensions. Our findings indicate that a more refined notion of connectivity (mutual k-Nearest Neighbors with minimum spanning tree) together with a flexible method of constructing the local neighborhood (Path Neighbors), can achieve a much better representation than default UMAP, as measured by downstream clustering performance.
翻译:T-SNE 和 UMAP 等基于地形的减少维度方法在高维数据中越来越成功和受欢迎。这些方法具有很强的数学基础,并且基于以下直觉:低维的地形学应该接近高维。鉴于初始地形结构是算法成功前的先导,这自然会提出一个问题:“良好的”地形结构是什么使维度降低?从这个角度看,将使我们能够设计出更好的算法,既考虑到地方结构,又考虑到全球结构。在以UMAP为重点的本文中,我们研究了节点连接(K-Nearest Neighearbors 相对于相互的 k-Nearst Neighbors ) 和相对邻里(通过路径相邻相邻的相邻结构) 和相对邻里(相对相邻的) 在减少维度方面的影响。我们通过对4个标准图像和文本数据集的广泛对比研究来探索这些概念;MNIST, FMNIST, 20NG, AG, 减为2和64个维度的维度。我们的研究结果表明,一个更精细的连接概念(m-K-Negh Negh Negh-Negh Beghbors ) 能够通过测量一个更灵活的区域图层结构,共同实现一个更精确的地面结构,通过一个更精确的地面图,通过一个更精确的底层图层图制式的地面图。