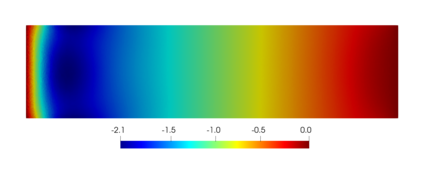
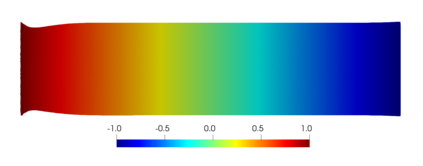
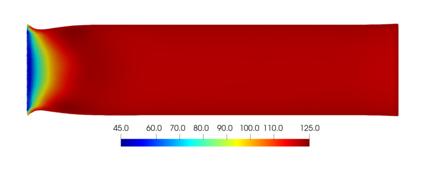
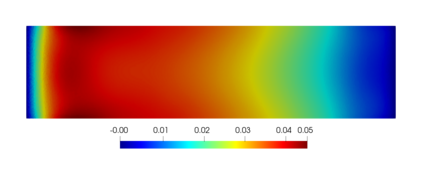
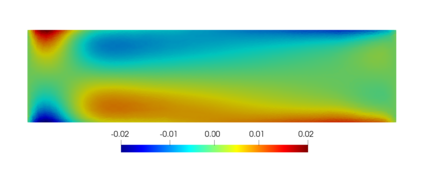
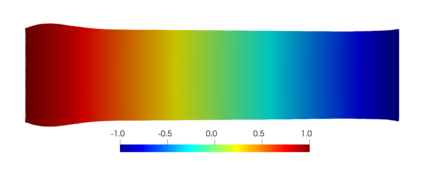
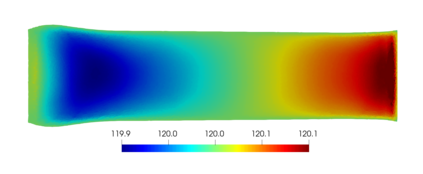
We present and analyze a discontinuous Galerkin method for the numerical modelling of the non-linear fully-coupled thermo-poroelastic problem. For the spatial discretization, we design a high-order discontinuous Galerkin method on polygonal and polyhedral grids based on a novel four-field formulation of the problem. To handle the non-linear convective transport term in the energy conservation equation we adopt a fixed-point linearization strategy. We perform a robust stability analysis for the linearized semi-discrete problem under mild requirements on the problem data. A priori hp-version error estimates in suitable energy norms are also derived. A complete set of numerical simulations is presented in order to validate the theoretical analysis, to inspect numerically the robustness properties, and to test the capability of the proposed method in a practical scenario inspired by a geothermal problem.
翻译:我们提出并分析一种不连续的Galerkin方法,用于模拟非线性完全混合的热聚氨酯问题的数字模型。关于空间离散,我们根据对问题的新颖的四边配方,设计了多角和多面网格的高分级不连续的Galerkin方法。为了处理节能方程式中的非线性对流运输术语,我们采用了固定点线性战略。我们根据对问题数据的温和要求,对线性半分解问题进行了稳健的稳定分析。还得出了适当能源规范中的先验 hp-version误差估计数。提出了一套完整的数字模拟,以验证理论分析,从数字上检查坚固性,并在地热问题引发的实际假设中测试拟议方法的能力。