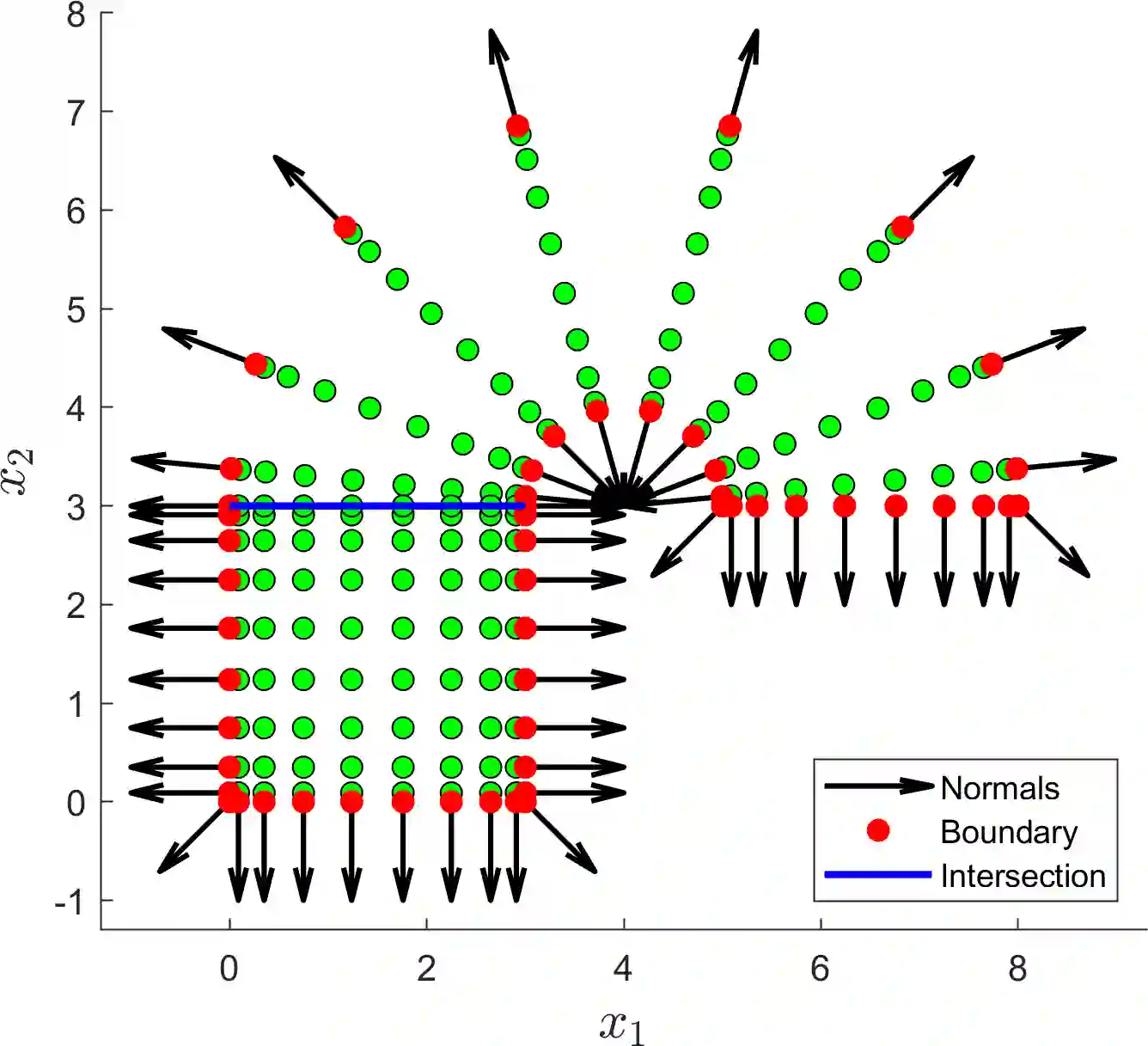
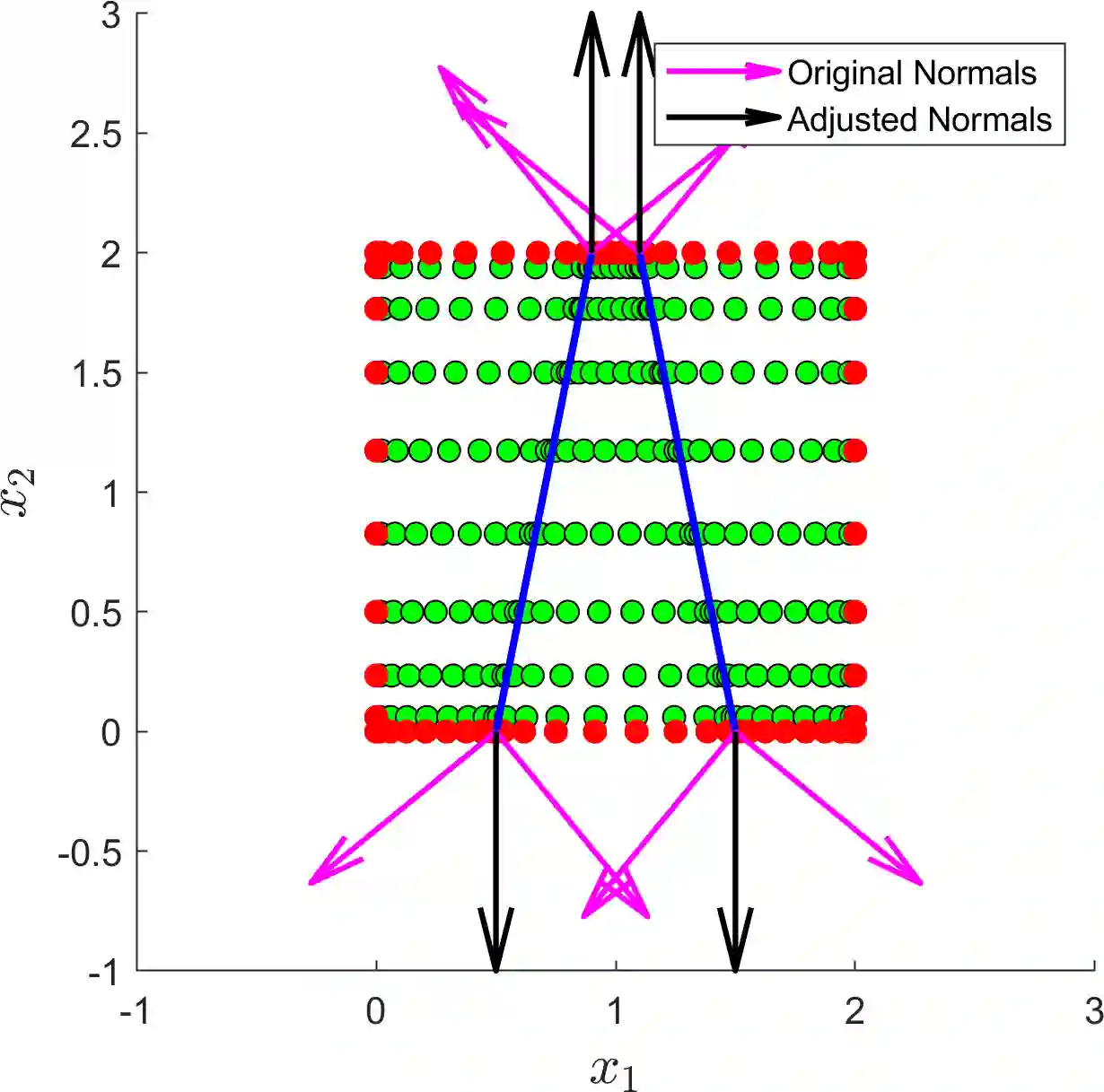
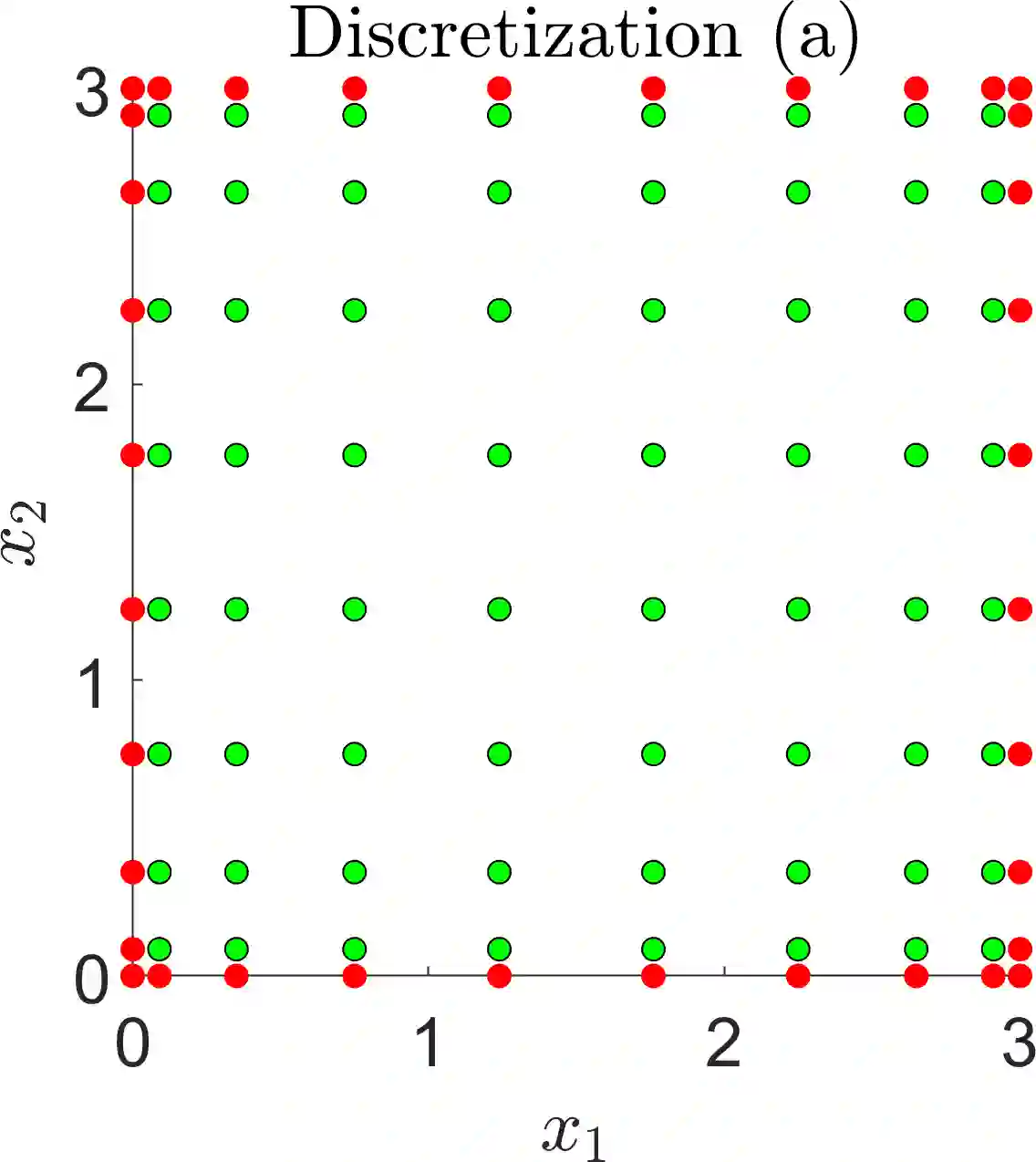
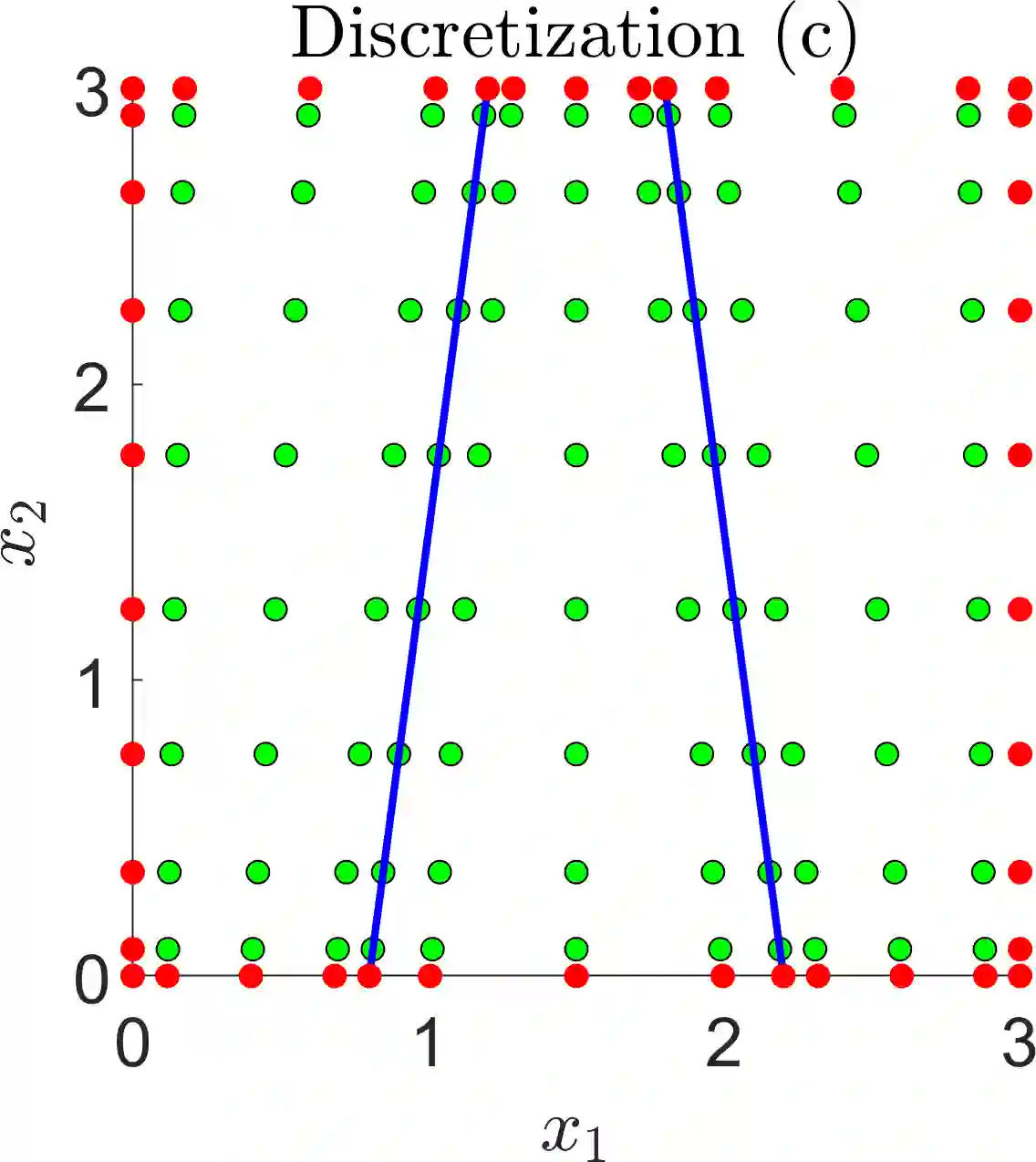
A numerical framework is developed to solve various types of PDEs on complicated domains, including steady and time-dependent, non-linear and non-local PDEs, with different boundary conditions that can also include non-linear and non-local terms. This numerical framework, called MultiShape, is a class in Matlab, and the software is open source. We demonstrate that MultiShape is compatible with other numerical methods, such as differential--algebraic equation solvers and optimization algorithms. The numerical implementation is designed to be user-friendly, with most of the set-up and computations done automatically by MultiShape and with intuitive operator definition, notation, and user-interface. Validation tests are presented, before we introduce three examples motivated by applications in Dynamic Density Functional Theory and PDE-constrained optimization, illustrating the versatility of the method.
翻译:开发了一个数字框架,以解决复杂领域的各类项目设计文件,包括稳定和时间依赖、非线性和非本地性项目设计文件,其不同的边界条件也可以包括非线性和非本地术语。这个数字框架称为多Shape,是Matlab中的一个类别,软件是开放源。我们证明,多Shape与其他数字方法兼容,如差异-高位方程解算器和优化算法。数字实施的设计是方便用户的,大多数设置和计算都是由多Shape自动完成的,并且由直观操作者定义、标记和用户界面来进行。在我们介绍由动态密度功能理论和受PDE制约的优化的应用驱动的三个实例之前,先提出验证测试,说明该方法的多功能性。