On the Robustness of Bayesian Neural Networks to Adversarial Attacks

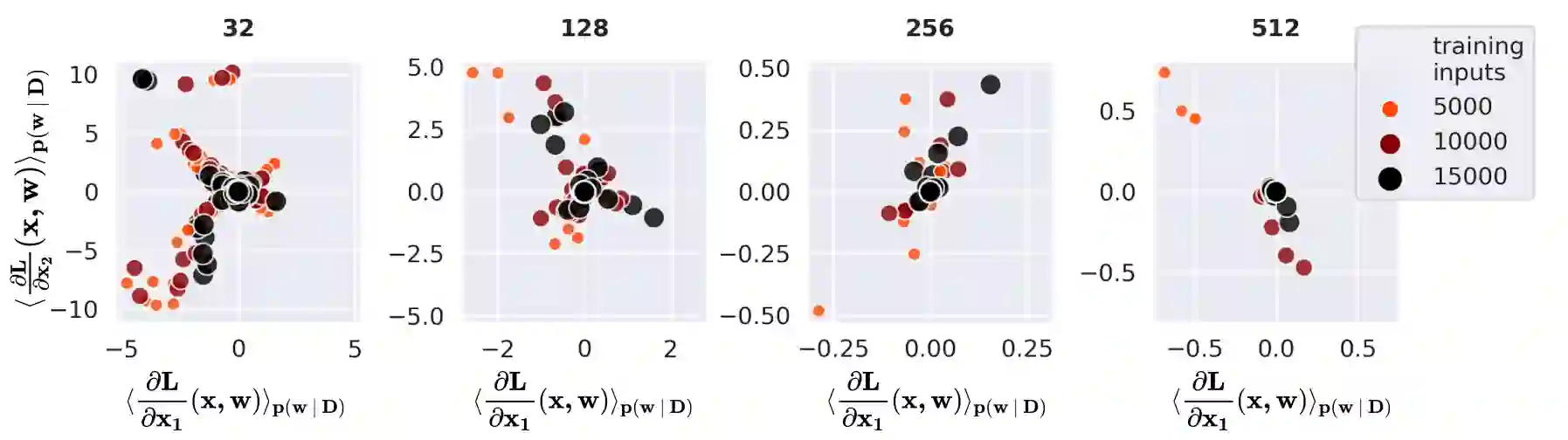
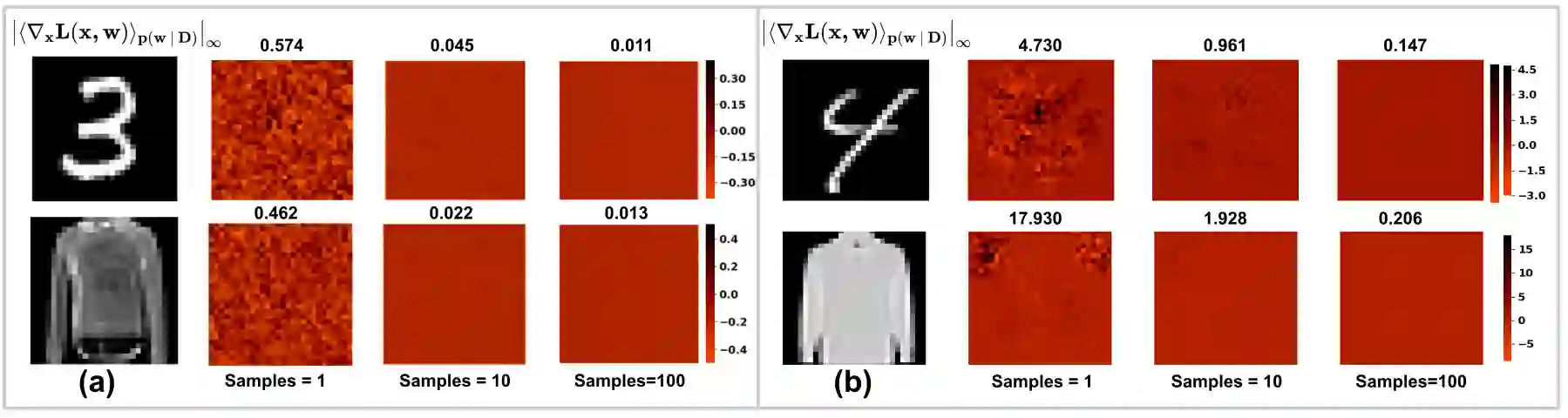
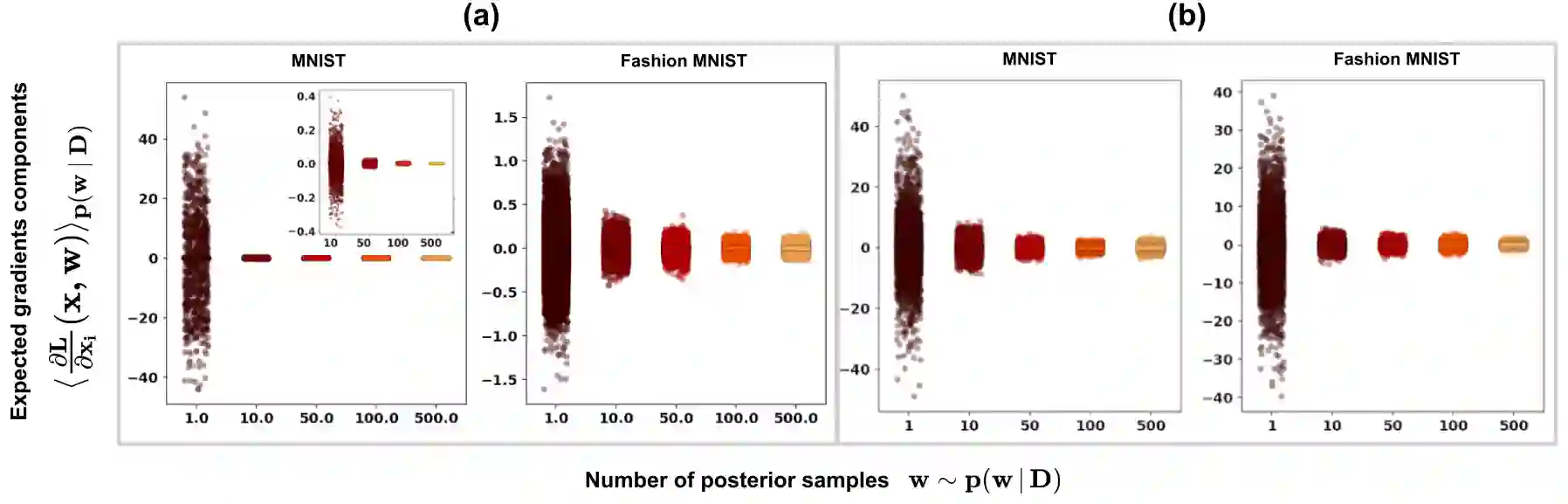
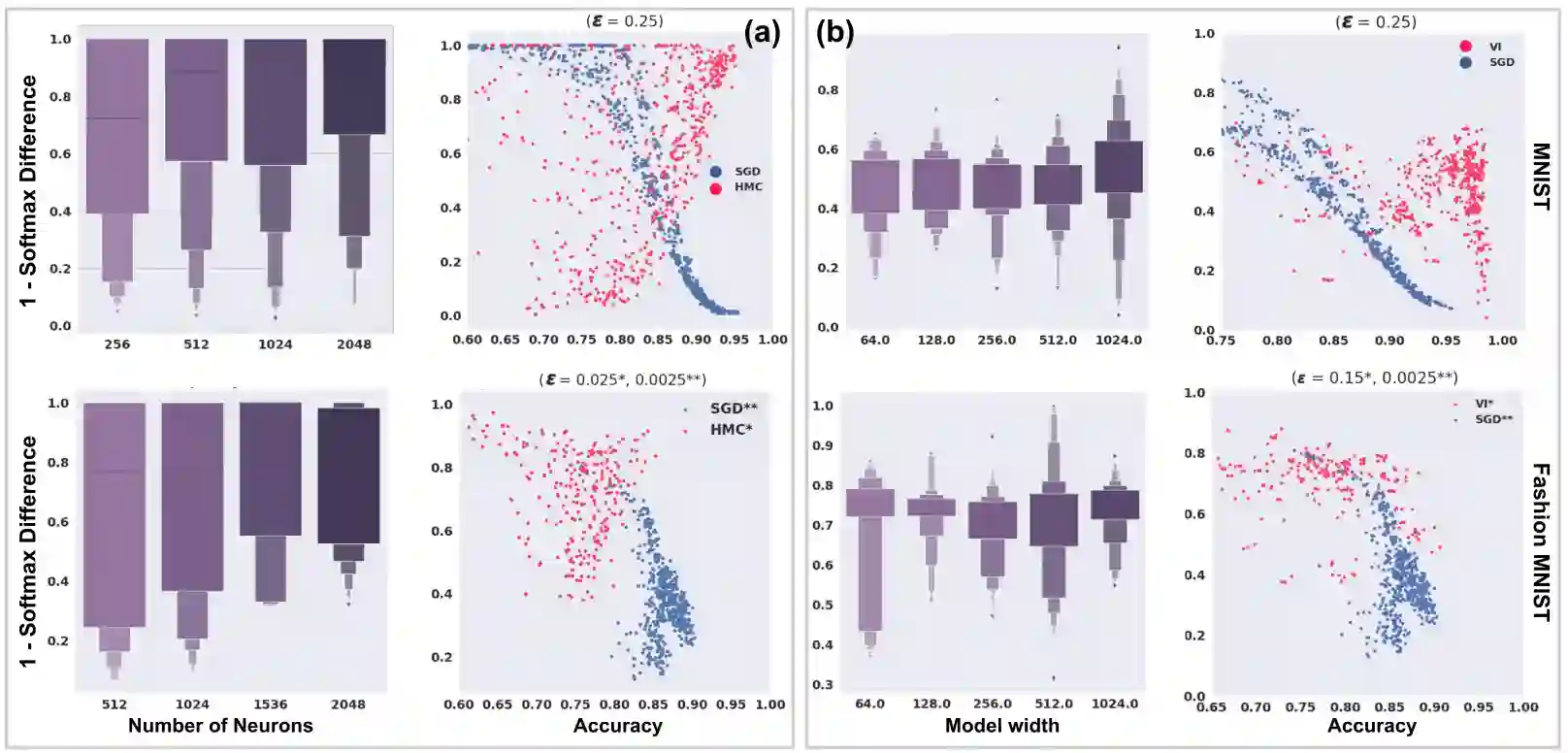
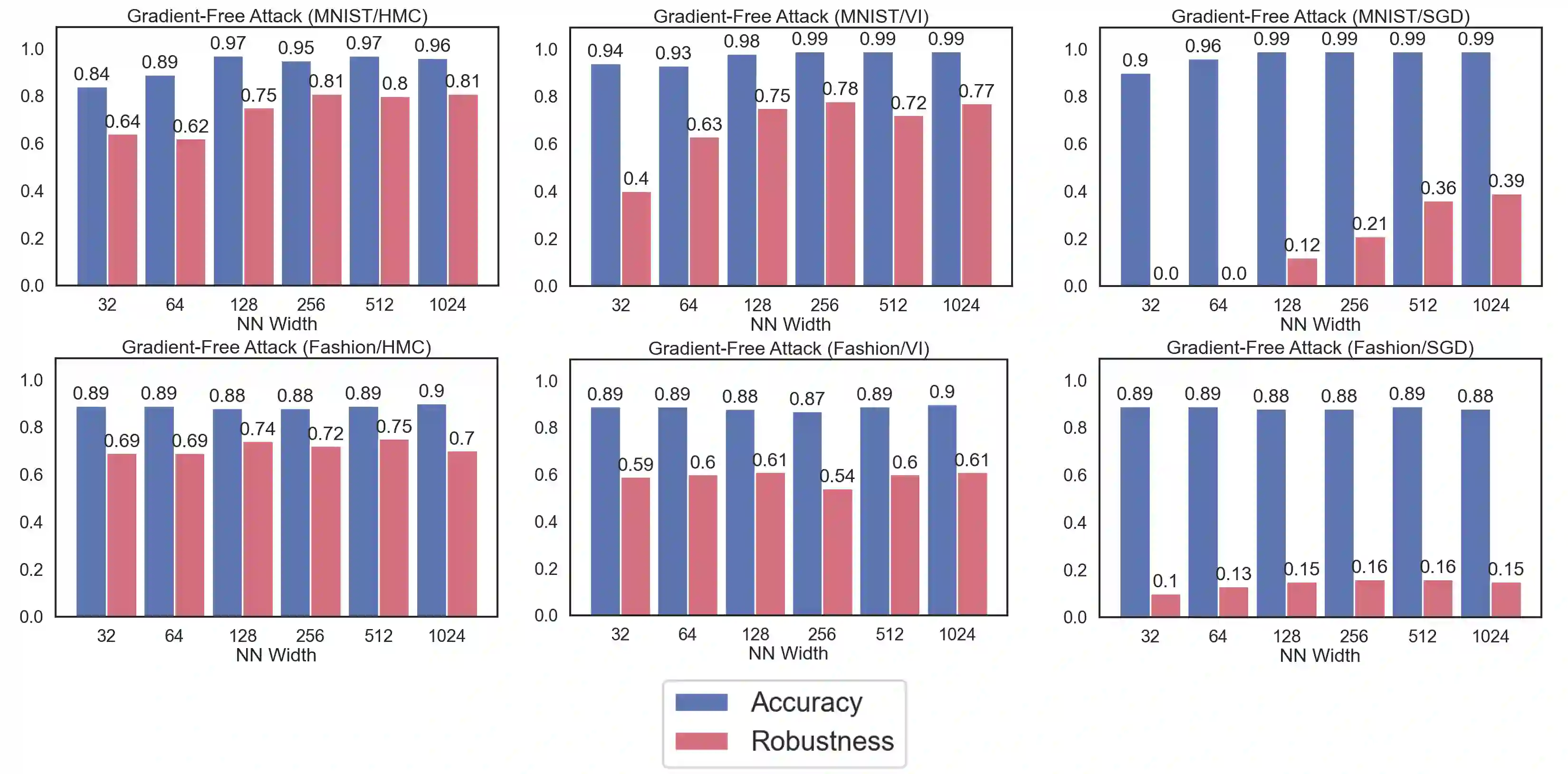
Vulnerability to adversarial attacks is one of the principal hurdles to the adoption of deep learning in safety-critical applications. Despite significant efforts, both practical and theoretical, training deep learning models robust to adversarial attacks is still an open problem. In this paper, we analyse the geometry of adversarial attacks in the large-data, overparameterized limit for Bayesian Neural Networks (BNNs). We show that, in the limit, vulnerability to gradient-based attacks arises as a result of degeneracy in the data distribution, i.e., when the data lies on a lower-dimensional submanifold of the ambient space. As a direct consequence, we demonstrate that in this limit BNN posteriors are robust to gradient-based adversarial attacks. Crucially, we prove that the expected gradient of the loss with respect to the BNN posterior distribution is vanishing, even when each neural network sampled from the posterior is vulnerable to gradient-based attacks. Experimental results on the MNIST, Fashion MNIST, and half moons datasets, representing the finite data regime, with BNNs trained with Hamiltonian Monte Carlo and Variational Inference, support this line of arguments, showing that BNNs can display both high accuracy on clean data and robustness to both gradient-based and gradient-free based adversarial attacks.