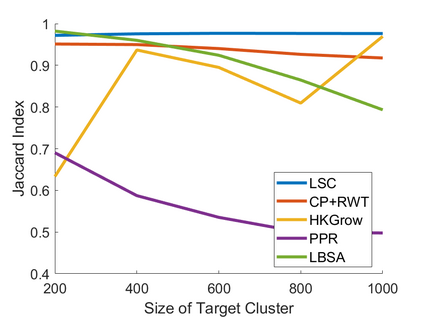
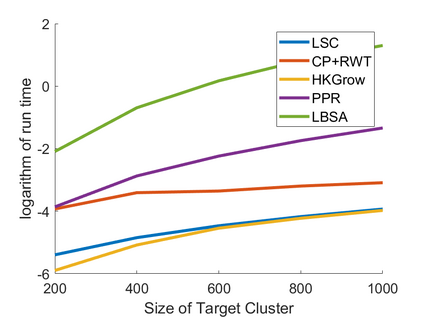
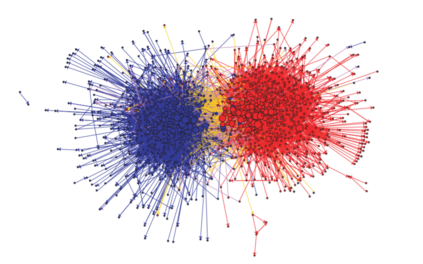
A least squares semi-supervised local clustering algorithm based on the idea of compressed sensing is proposed to extract clusters from a graph with known adjacency matrix. The algorithm is based on a two-stage approach similar to the one in \cite{LaiMckenzie2020}. However, under a weaker assumption and with less computational complexity than the one in \cite{LaiMckenzie2020}, the algorithm is shown to be able to find a desired cluster with high probability. The ``one cluster at a time" feature of our method distinguishes it from other global clustering methods. Several numerical experiments are conducted on the synthetic data such as stochastic block model and real data such as MNIST, political blogs network, AT\&T and YaleB human faces data sets to demonstrate the effectiveness and efficiency of our algorithm.
翻译:以压缩感测为理念的最小平方半监督本地群集算法建议从已知相邻矩阵的图表中提取群集。 算法基于类似于\ cite{ LaiMckenzie2020} 的两阶段方法。 但是, 在较弱的假设和计算复杂性低于\ cite{LaiMckenzie20} 的假设下, 算法证明能够找到一个高概率的预期群集。 我们方法的“ one 群集” 特征将其与其他全球群集方法区分开来。 对合成数据进行了数项实验, 如混凝土块模型和像 MNIST、政治博客网络、 AT ⁇ T 和 耶鲁布人脸数据集等真实数据, 以证明我们的算法的有效性和效率 。