An MP-DWR method for $h$-adaptive finite element methods

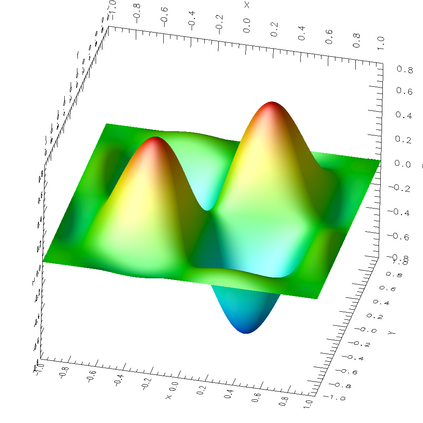
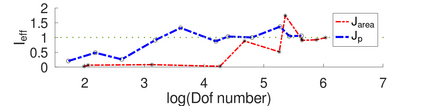
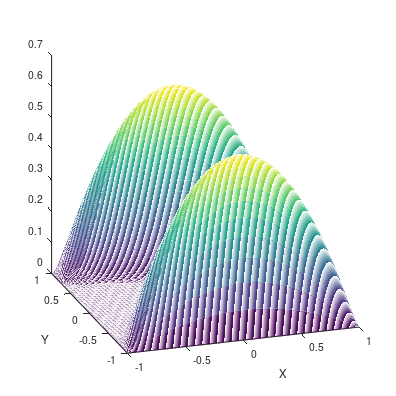
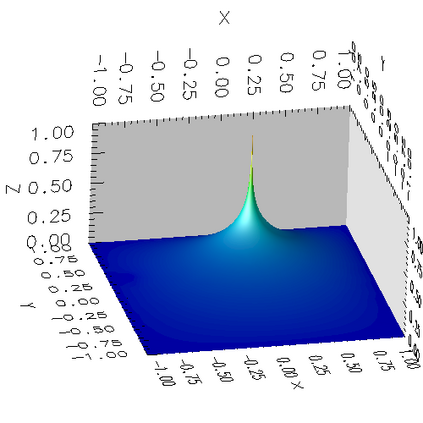
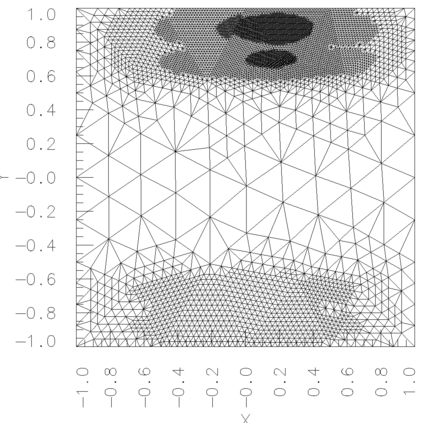
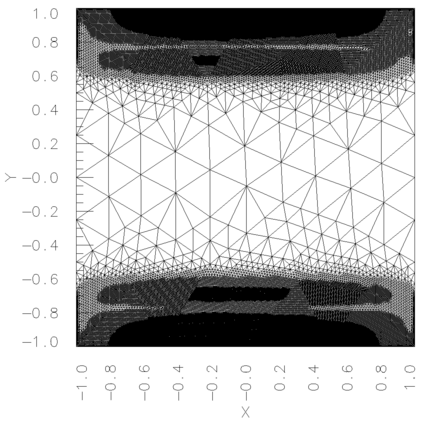
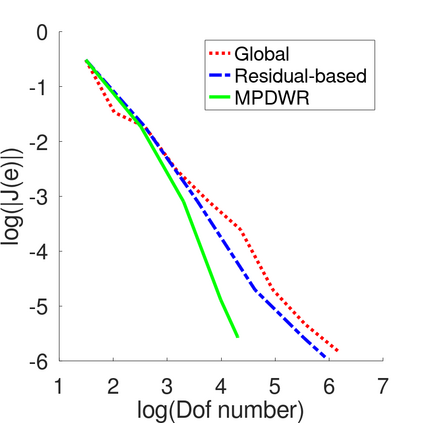
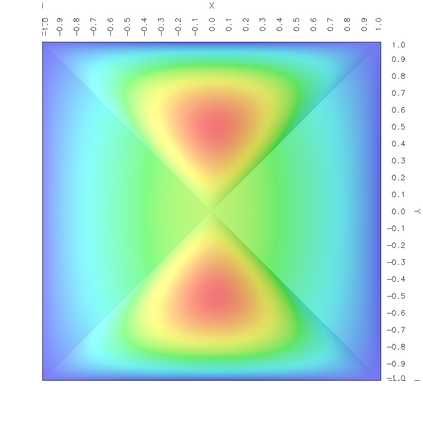
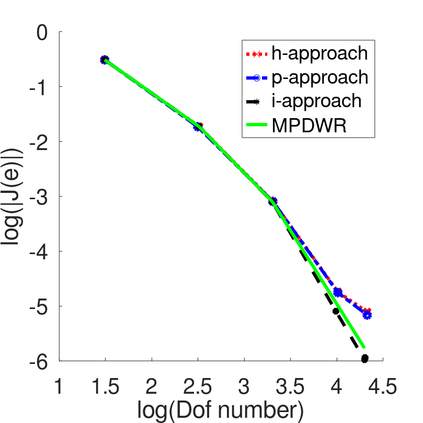
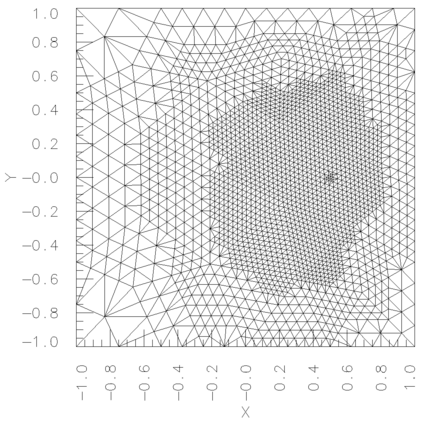
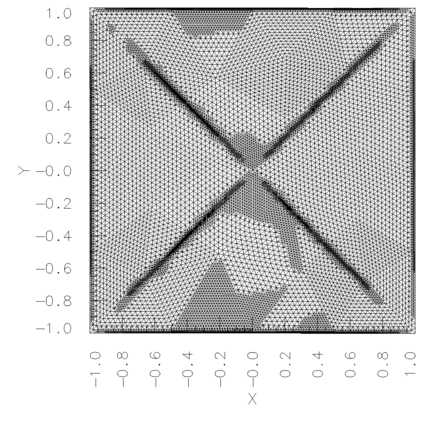
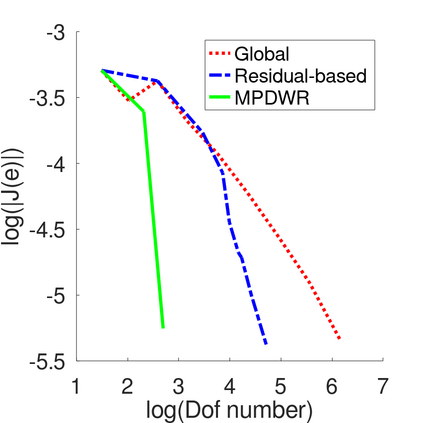
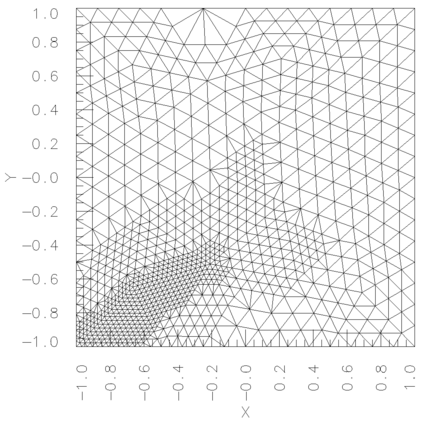
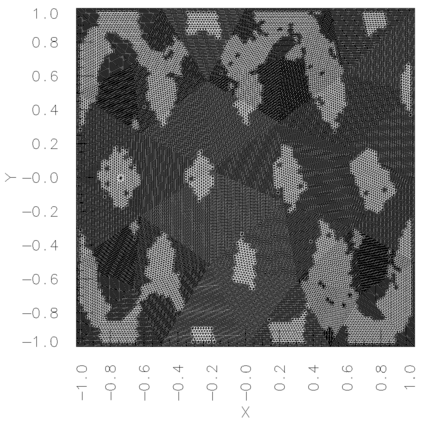
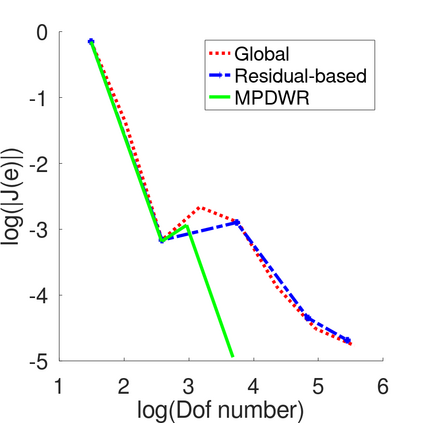
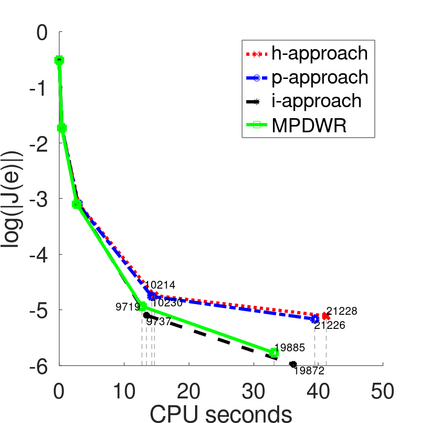
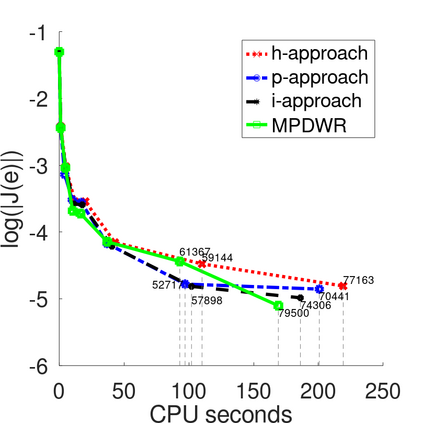
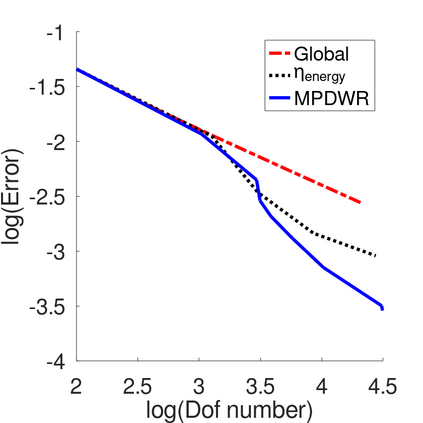
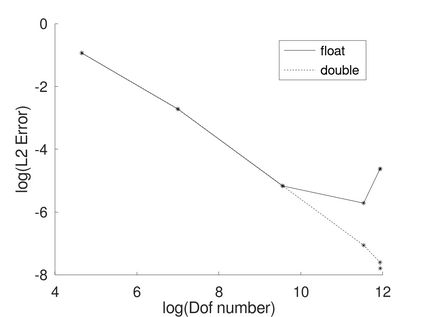
In a dual weighted residual method based on the finite element framework, the Galerkin orthogonality is an issue which prevents solving the dual equation in the same space to the one for the primal equation. In the literature, there have been two popular approaches to construct a new space for the dual problem, i.e., refining mesh grids ($h$-approach) and raising the order of approximate polynomials ($p$-approach). In this paper, a novel approach is proposed for the purpose based on the multiple-precision technique, i.e., the construction of the new finite element space is based on the same configuration to the one for the primal equation, except for the precision used for the finite arithmetic calculation in the computer. The feasibility of such a new approach is discussed in detail in the paper, from which it can be seen that the Galerkin orthogonality is avoided effectively. A main feature of our approach is that the remarkable improvement on both the efficiency and the storage can be expected compared with the $h$-approach and the $p$-approach, since necessary operations such as remeshing, regenerating finite elements and their integration environments in classical approaches can be avoided in the algorithm. A number of numerical examples successfully confirm the feature of our method, in which upto an order of magnitude improvement on the CPU time can even be observed in generating the error indicator, compared with classical $h$-approach and $p$-approach. It is worth mentioning that the performance of our approach is comparable with the one through a higher order interpolation ($i$-approach) in the literature. The combination of two approaches is believed a way to further enhancing the efficiency of the dual weighted residual method.