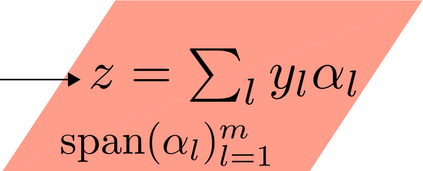Non-convex methods for linear inverse problems with low-dimensional models have emerged as an alternative to convex techniques. We propose a theoretical framework where both finite dimensional and infinite dimensional linear inverse problems can be studied. We show how the size of the the basins of attraction of the minimizers of such problems is linked with the number of available measurements. This framework recovers known results about low-rank matrix estimation and off-the-grid sparse spike estimation, and it provides new results for Gaussian mixture estimation from linear measurements. keywords: low-dimensional models, non-convex methods, low-rank matrix recovery, off-the-grid sparse recovery, Gaussian mixture model estimation from linear measurements.
翻译:对于低维模型的线性反问题,出现了非隐形方法,作为共形技术的替代。我们提出了一个理论框架,可以研究有限维和无限维线性线性反问题。我们展示了这类问题最小化者的吸引力盆地的规模如何与现有测量数量挂钩。这个框架恢复了已知的关于低级矩阵估计和离电网稀释性峰值估计的结果,为从线性测量得出的高斯混合物估计提供了新的结果。关键词:低维模型、非共形方法、低位矩阵恢复、离电网稀释性恢复、高斯混合模型从线性测量得出的估计。