Runtime analysis of the (mu+1)-EA on the Dynamic BinVal function

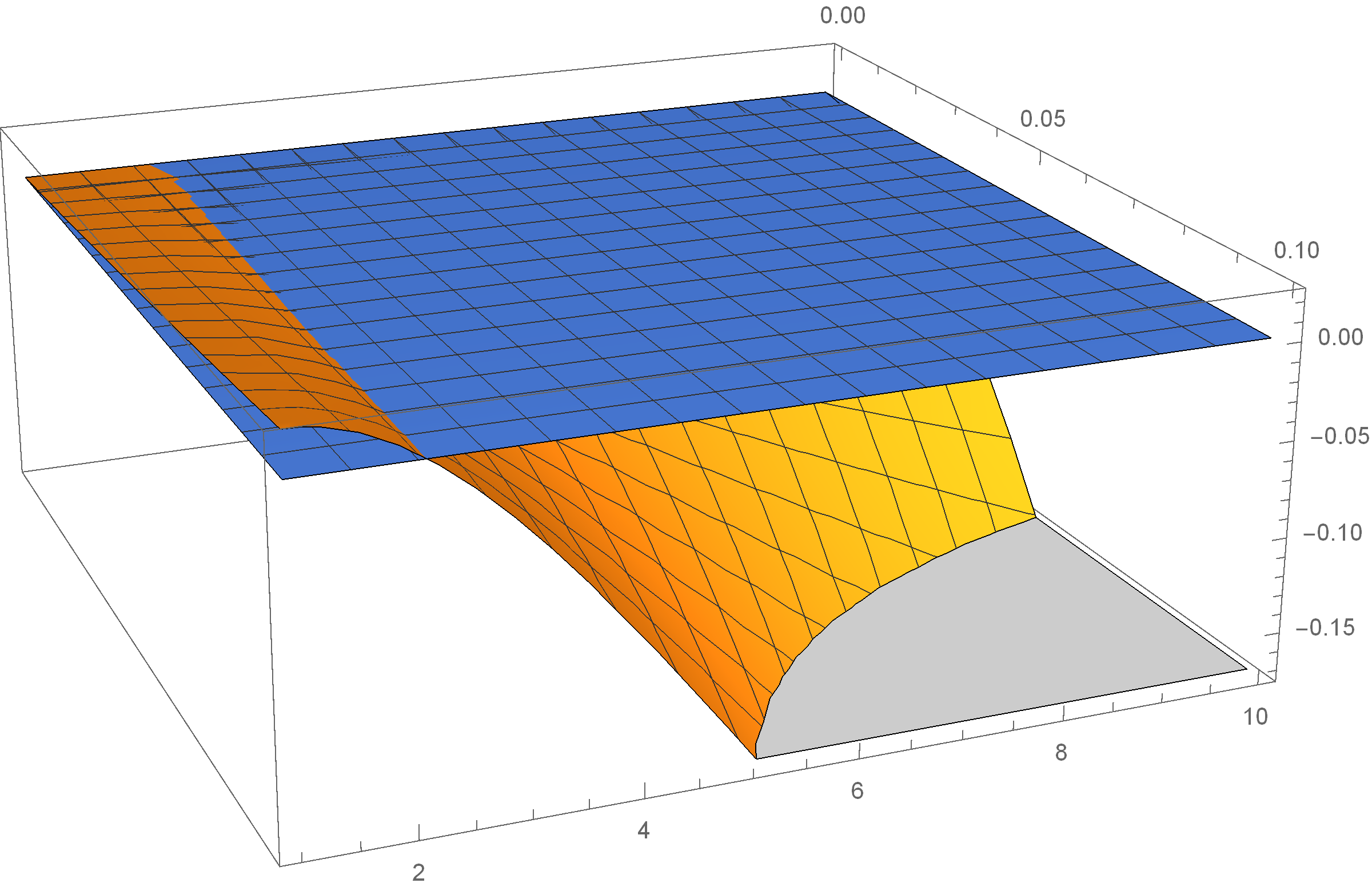
We study evolutionary algorithms in a dynamic setting, where for each generation a different fitness function is chosen, and selection is performed with respect to the current fitness function. Specifically, we consider Dynamic BinVal, in which the fitness functions for each generation is given by the linear function BinVal, but in each generation the order of bits is randomly permuted. For the (1+1)-EA it was known that there is an efficiency threshold $c_0$ for the mutation parameter, at which the runtime switches from quasilinear to exponential. A previous empirical evidence suggested that for larger population size $\mu$, the threshold may increase. We prove that this is at least the case in an $\varepsilon$-neighborhood around the optimum: the threshold of the (\mu+1)-EA becomes arbitrarily large if the $\mu$ is chosen large enough. However, the most surprising result is obtained by a second order analysis for $\mu=2$: the threshold INcreases with increasing proximity to the optimum. In particular, the hardest region for optimization is NOT around the optimum.