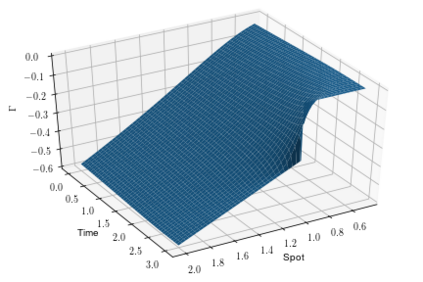
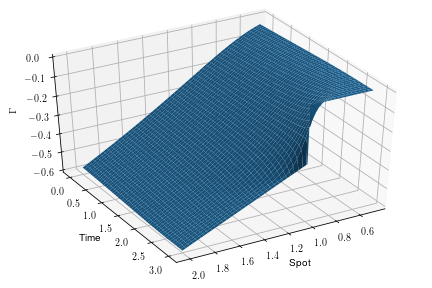
Variance reduction techniques are of crucial importance for the efficiency of Monte Carlo simulations in finance applications. We propose the use of neural SDEs, with control variates parameterized by neural networks, in order to learn approximately optimal control variates and hence reduce variance as trajectories of the SDEs are being simulated. We consider SDEs driven by Brownian motion and, more generally, by L\'{e}vy processes including those with infinite activity. For the latter case, we prove optimality conditions for the variance reduction. Several numerical examples from option pricing are presented.
翻译:减少差异技术对于蒙特卡洛模拟金融应用的效率至关重要。我们提议使用神经SDE,由神经网络设定控制变异参数,以学习大约最佳的控制变异,从而随着SDE的轨迹被模拟而减少差异。我们认为,由布朗运动驱动的SDEs,以及更一般地说,由L\'{e}动态驱动的SDEs,包括无穷活动的过程。对于后一种情况,我们证明有最佳的减少差异条件。提出了几个选择定价数字的例子。