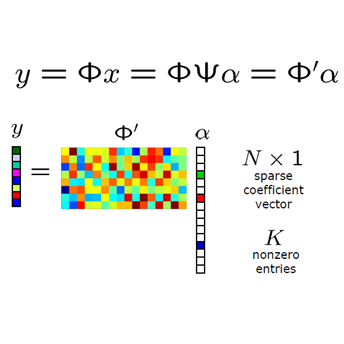
Coherent Ising Machine (CIM) is a network of optical parametric oscillators that solves combinatorial optimization problems by finding the ground state of an Ising Hamiltonian. As a practical application of CIM, Aonishi et al. proposed a quantum-classical hybrid system to solve optimization problems of L0-regularization-based compressed sensing (L0RBCS). Gunathilaka et al. has further enhanced the accuracy of the system. However, the computationally expensive CIM's stochastic differential equations (SDEs) limit the use of digital hardware implementations. As an alternative to Gunathilaka et al.'s CIM SDEs used previously, we propose using the mean-field CIM (MF-CIM) model, which is a physics-inspired heuristic solver without quantum noise. MF-CIM surmounts the high computational cost due to the simple nature of the differential equations (DEs). Furthermore, our results indicate that the proposed model has similar performance to physically accurate SDEs in both artificial and magnetic resonance imaging data, paving the way for implementing CIM-based L0RBCS on digital hardware such as Field Programmable Gate Arrays (FPGAs).
翻译:暂无翻译