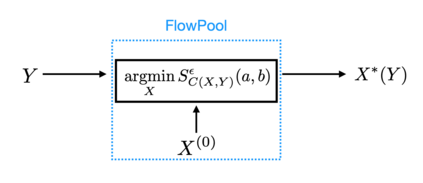
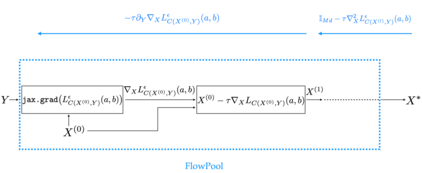
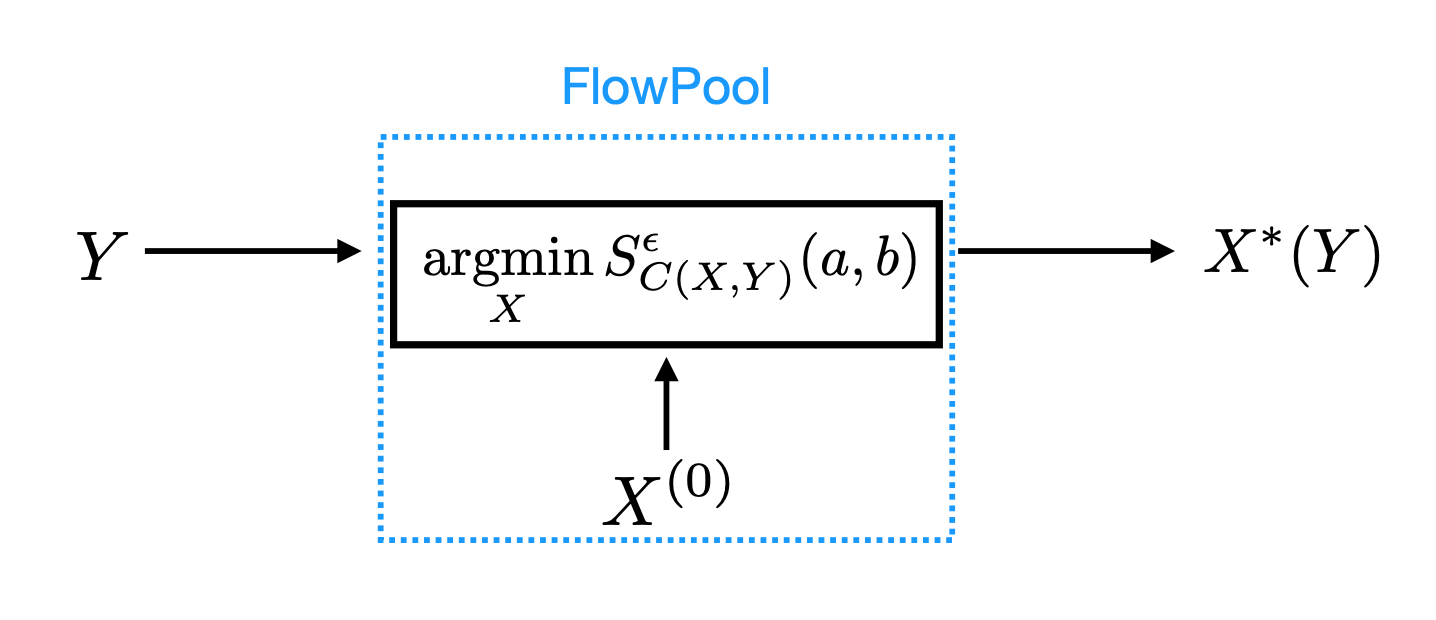
In several machine learning tasks for graph structured data, the graphs under consideration may be composed of a varying number of nodes. Therefore, it is necessary to design pooling methods that aggregate the graph representations of varying size to representations of fixed size which can be used in downstream tasks, such as graph classification. Existing graph pooling methods offer no guarantee with regards to the similarity of a graph representation and its pooled version. In this work, we address this limitation by proposing FlowPool, a pooling method that optimally preserves the statistics of a graph representation to its pooled counterpart by minimising their Wasserstein distance. This is achieved by performing a Wasserstein gradient flow with respect to the pooled graph representation. Our method relies on a versatile implementation which can take into account the geometry of the representation space through any ground cost and computes the gradient of the Wasserstein distance with automatic differentiation. We propose the differentiation of the Wasserstein flow layer using an implicit differentiation scheme. Therefore, our pooling method is amenable to automatic differentiation and can be integrated in end-to-end deep learning architectures. Further, FlowPool is invariant to permutations and can therefore be combined with permutation equivariant feature extraction layers in GNNs in order to obtain predictions that are independent of the ordering of the nodes. Experimental results demonstrate that our method leads to an increase in performance compared to existing pooling methods when evaluated on graph classification.
翻译:在图形结构化数据的若干机器学习任务中,审议中的图表可能由不同数目的节点组成。因此,有必要设计汇集方法,将不同大小的图形表达方式与可用于下游任务的固定大小的表示形式(如图表分类)合并起来。现有的图形集合方法无法保证图形表达方式及其集合版本的相似性。在这项工作中,我们提出花pool这一集合方法来应对这一局限性,该方法通过尽可能缩小其瓦塞斯坦距离,最佳地将图表代表形式的统计数据保存到其集合对应方。这是通过对集合图形表示方式进行瓦塞斯坦梯度流动实现的。我们的方法依赖于多种功能性实施,该方法可以通过任何地面成本考虑到代表空间的几何结构,并用自动差异化来计算瓦塞斯坦距离的梯度。我们建议使用隐含的差别化办法区分瓦塞斯坦流层。因此,我们的集合方法可以自动区分,并将图表的统计方式整合到最终到深层次学习结构中。此外,流动波尔是难以变量的,因此,在对正轨方法进行独立分析时,可以将模型进行对比,以便对比地分析结果。