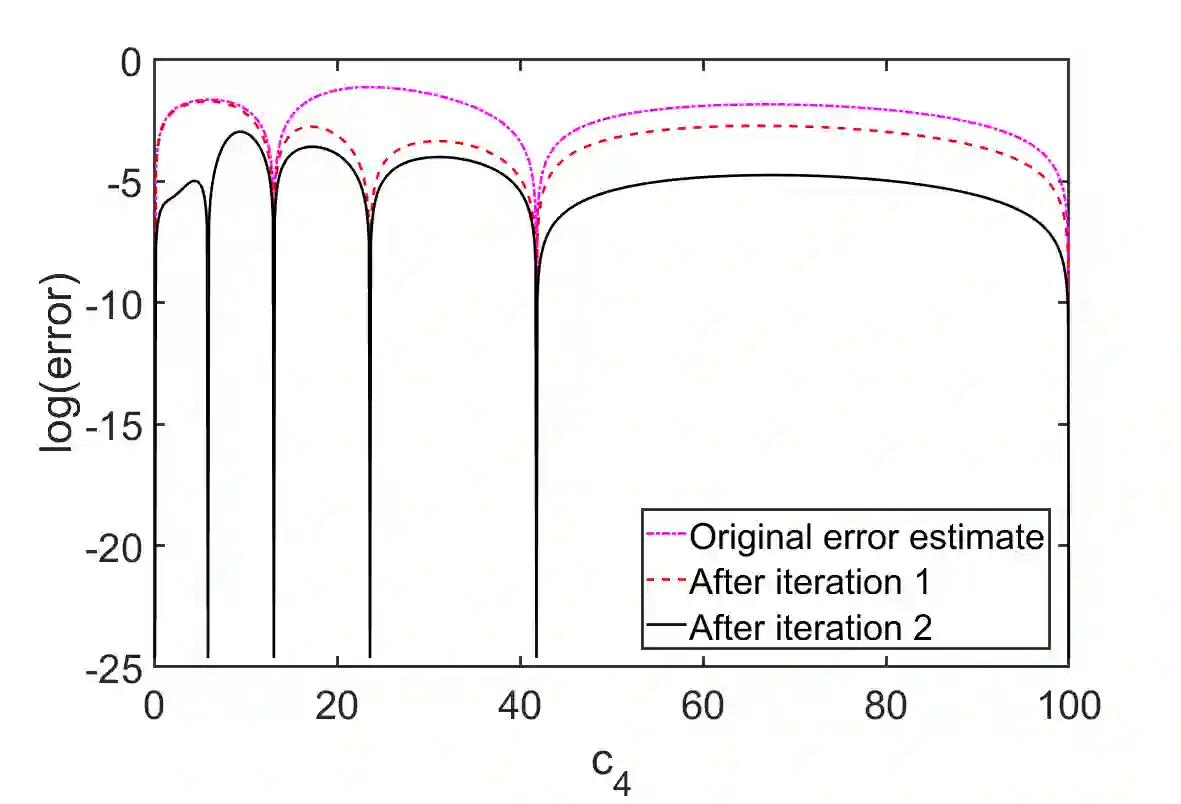
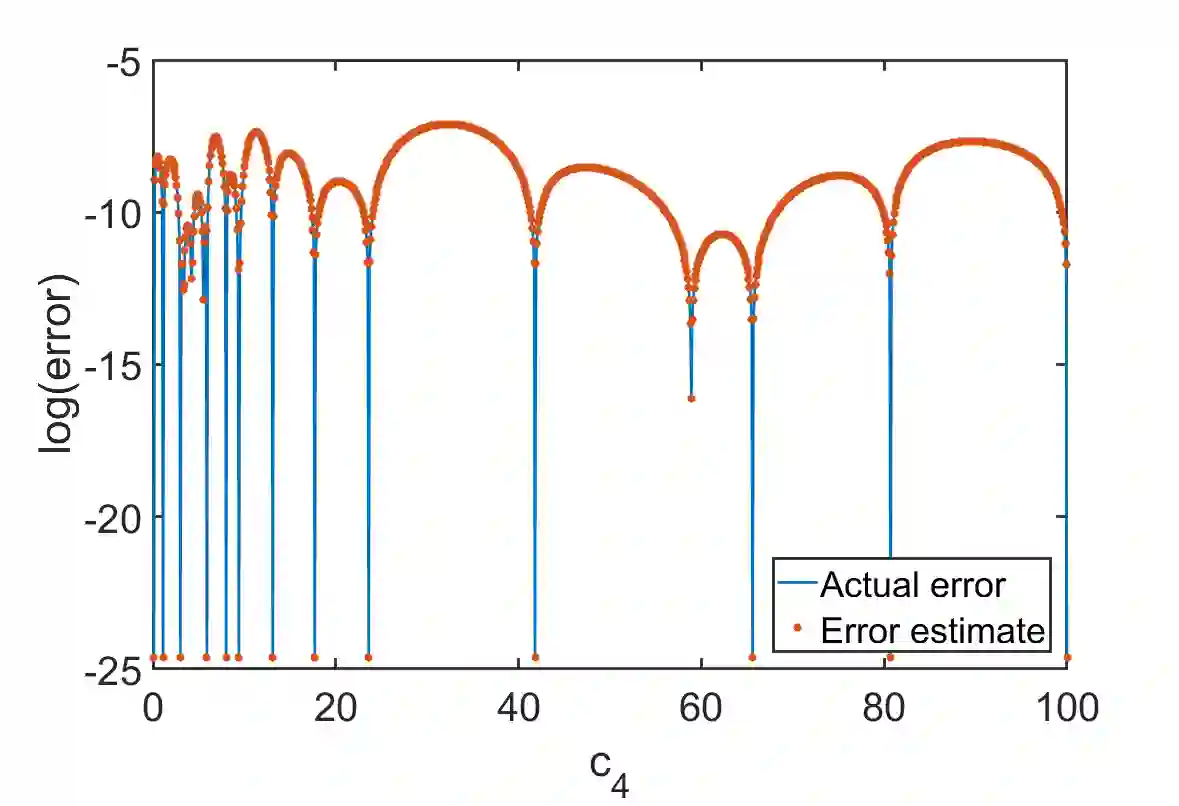
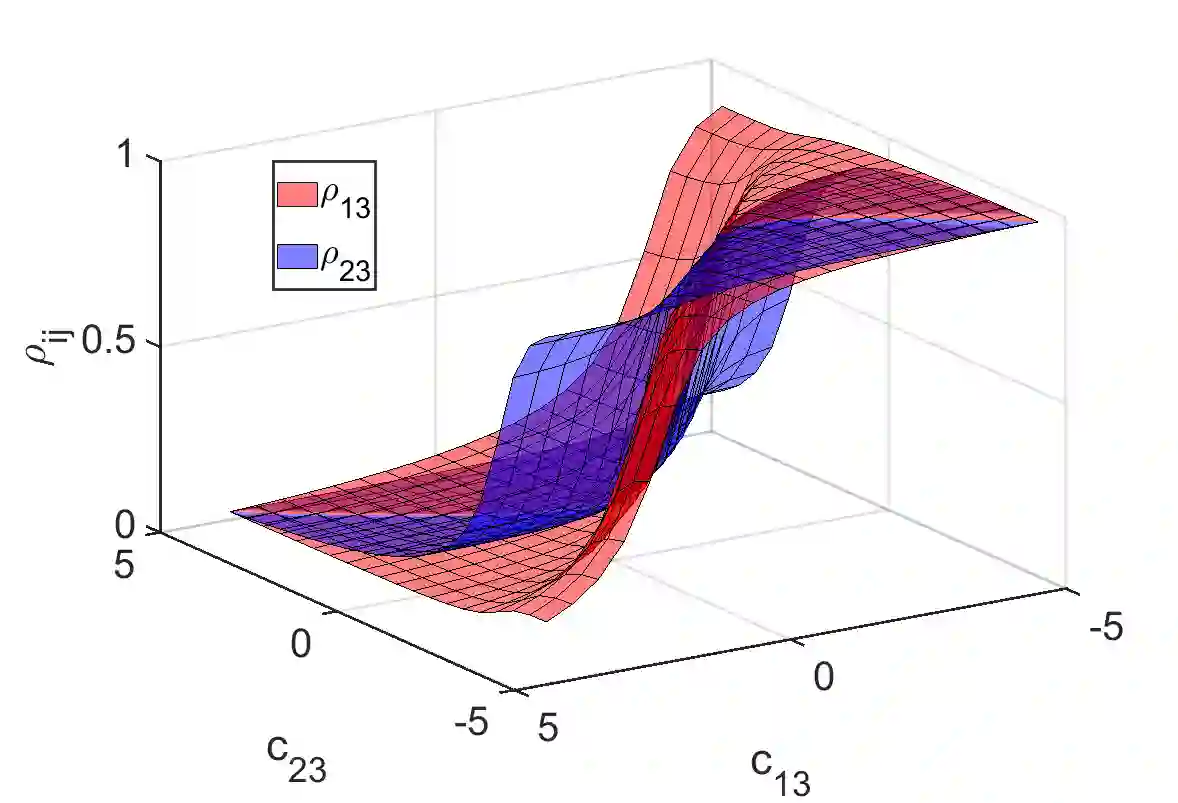
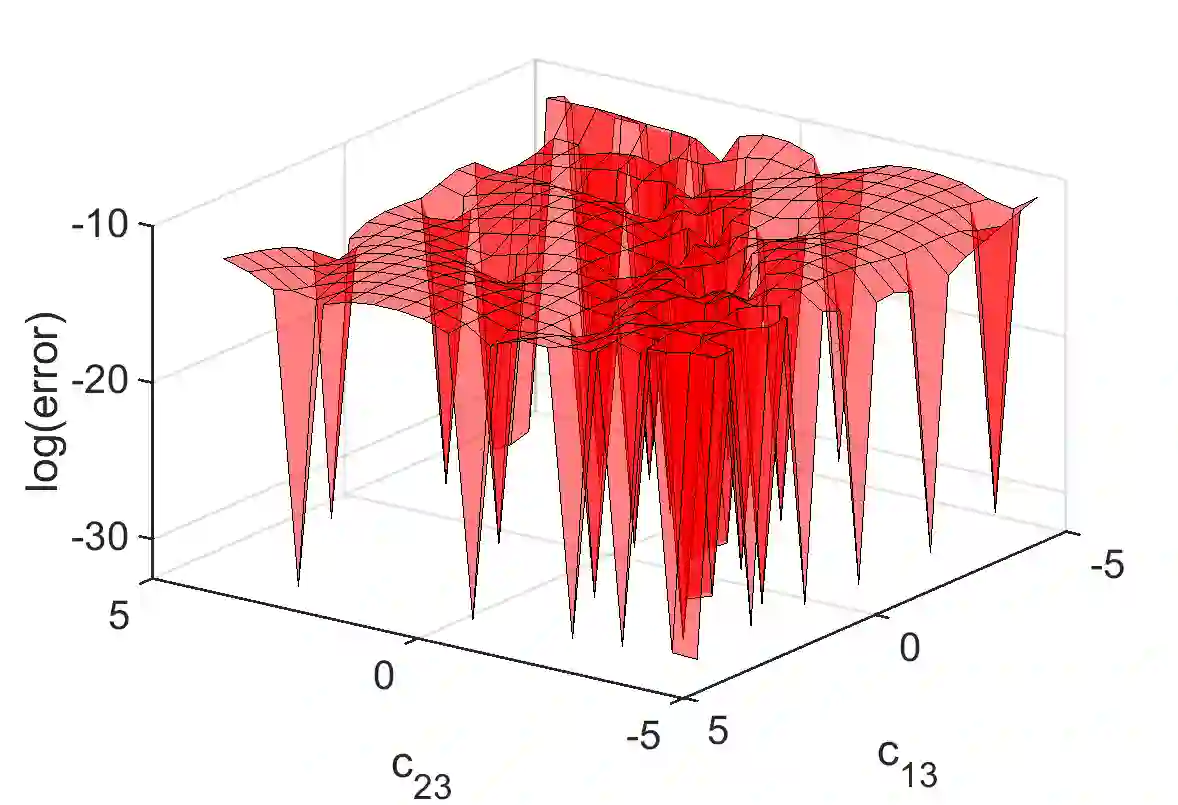
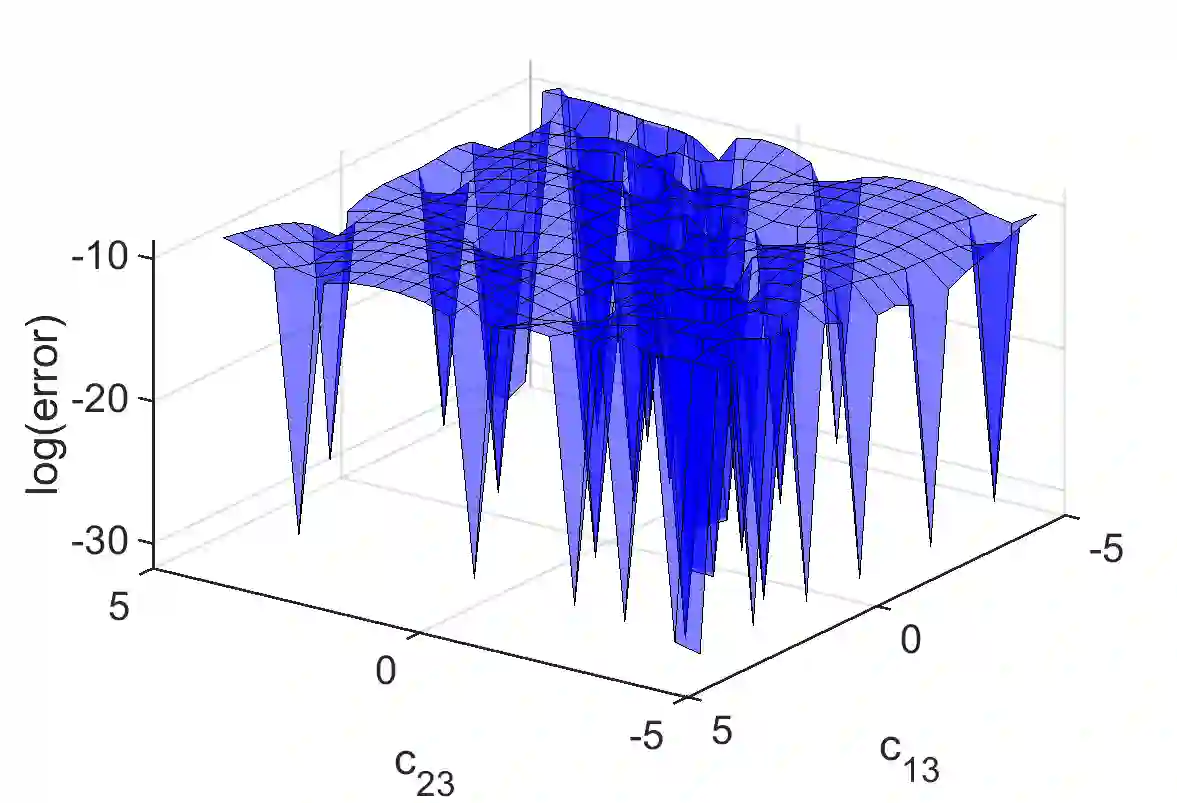
Emulators that can bypass computationally expensive scientific calculations with high accuracy and speed can enable new studies of fundamental science as well as more potential applications. In this work we focus on solving a system of constraint equations efficiently using a new machine learning approach that we call self-learning emulation. A self-learning emulator is an active learning protocol that can rapidly solve a system of equations over some range of control parameters. The key ingredient is a fast estimate of the emulator error that becomes progressively more accurate as the emulator improves. This acceleration is possible because the emulator itself is used to estimate the error, and we illustrate with two examples. The first uses cubic spline interpolation to find the roots of a polynomial with variable coefficients. The second example uses eigenvector continuation to find the eigenvectors and eigenvalues of a large Hamiltonian matrix that depends on several control parameters. We envision future applications of self-learning emulators for solving systems of algebraic equations, linear and nonlinear differential equations, and linear and nonlinear eigenvalue problems.
翻译:能够绕过计算成本高昂的科学计算,且精度和速度高的模拟器,可以促成对基础科学以及更多潜在应用进行新的研究。在这项工作中,我们侧重于使用我们称之为自我学习模拟的新型机器学习方法,高效率地解决制约方程系统。自学模拟器是一个积极的学习协议,可以快速解决一系列控制参数的方程系统。关键成分是对模拟器误差的快速估计,随着模拟器的改进,这种误差会逐渐变得更加准确。之所以能够加速,是因为模拟器本身被用来估计错误,我们用两个例子来说明。首先使用立方螺旋内插图来找出多数值的根。第二个例子是使用机源性延续来找到依赖若干控制参数的大型汉密尔顿仪矩阵的叶源和元值。我们设想未来应用自学模拟器来解决等式方程式、线性和非线性差方程式以及线性和非线性及非线性数值问题。
相关内容
Source: Apple - iOS 8