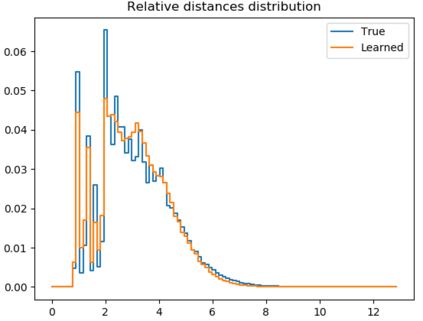
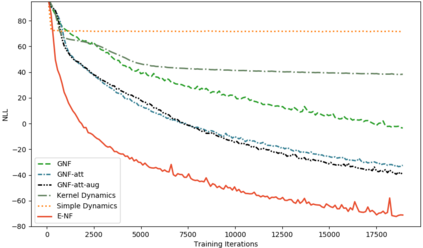
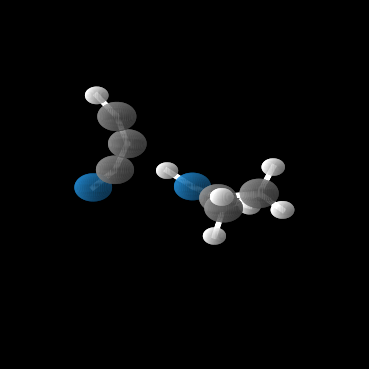
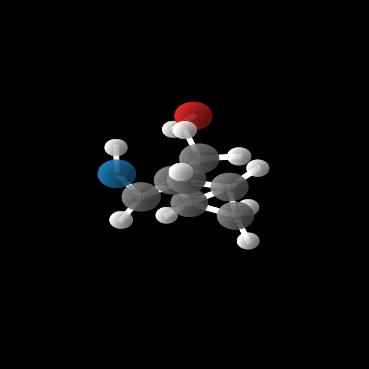
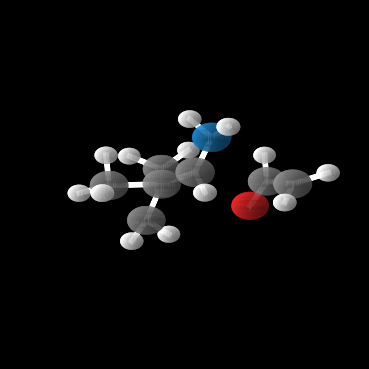
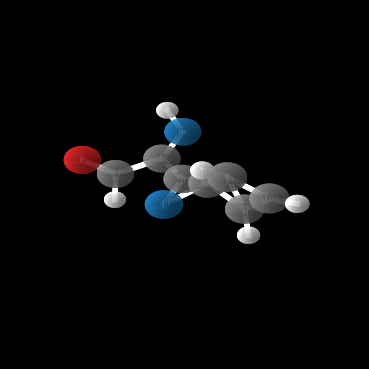
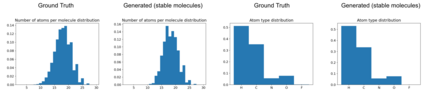
This paper introduces a generative model equivariant to Euclidean symmetries: E(n) Equivariant Normalizing Flows (E-NFs). To construct E-NFs, we take the discriminative E(n) graph neural networks and integrate them as a differential equation to obtain an invertible equivariant function: a continuous-time normalizing flow. We demonstrate that E-NFs considerably outperform baselines and existing methods from the literature on particle systems such as DW4 and LJ13, and on molecules from QM9 in terms of log-likelihood. To the best of our knowledge, this is the first flow that jointly generates molecule features and positions in 3D.
翻译:本文引入了一种归正模型,对欧几里得对称具有等同性:E(n) 均匀流(E-NFs) 。要构建 E-NFs,我们采用带有歧视性的 E(n) 图形神经网络,将其整合为一个差异方程式,以获得不可逆的等异功能:一个连续时间的正常流。我们证明,E-NFs大大超出DW4和LJ13等粒子系统以及QM9类分子在日志相似性方面的文献的基线和现有方法。据我们所知,这是在3D中联合生成分子特征和位置的第一批流动。