Hierarchically Clustered PCA, LLE, and CCA via a Convex Clustering Penalty

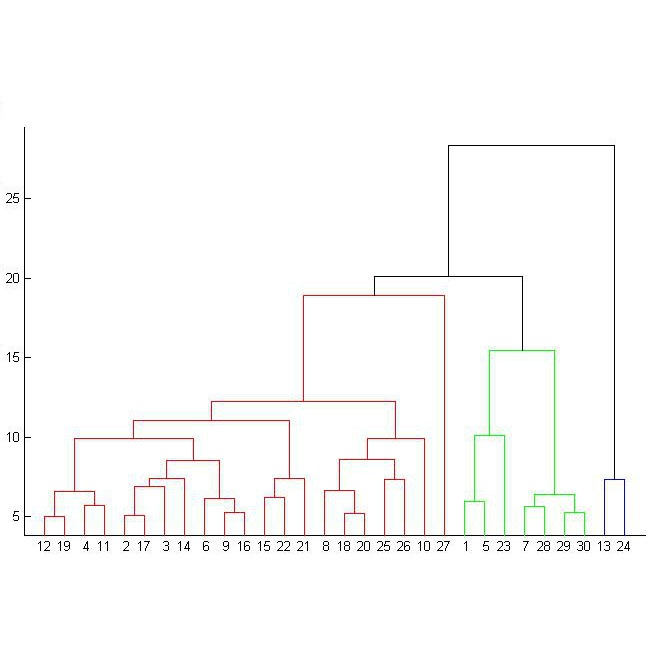
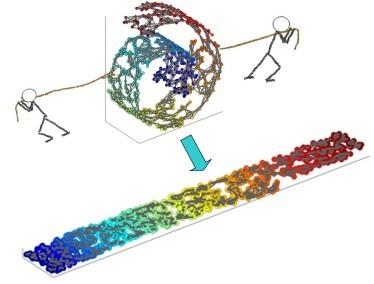
We introduce an unsupervised learning approach that combines the truncated singular value decomposition with convex clustering to estimate within-cluster directions of maximum variance/covariance (in the variables) while simultaneously hierarchically clustering (on observations). In contrast to previous work on joint clustering and embedding, our approach has a straightforward formulation, is readily scalable via distributed optimization, and admits a direct interpretation as hierarchically clustered principal component analysis (PCA), hierarchically clustered locally linear embedding (LLE), or hierarchically clustered canonical correlation analysis (CCA). Through numerical experiments and real-world examples relevant to precision medicine, we show that our approach outperforms traditional and contemporary clustering methods on both underdetermined problems ($p \gg N$ with tens of observations) and on large datasets (e.g., $N=100,000$) while yielding interpretable dendrograms of hierarchical per-cluster principal components or canonical variates.