Gaussian Whittle-Matérn fields on metric graphs

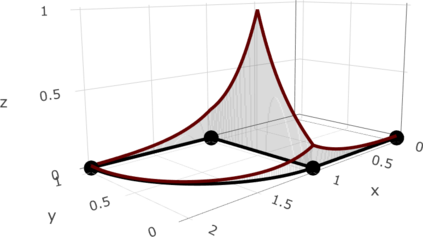
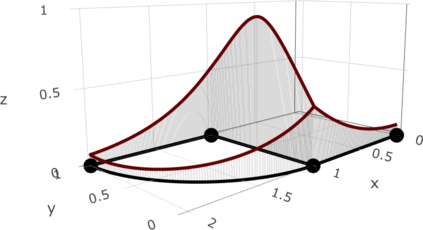
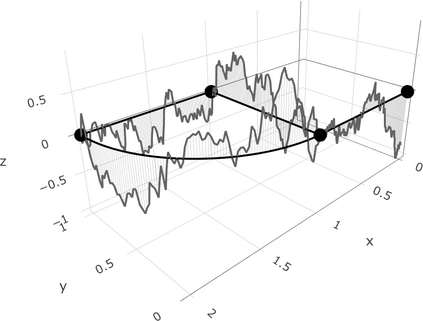
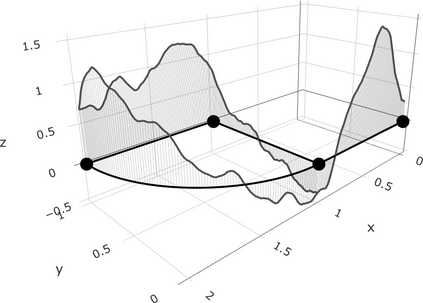
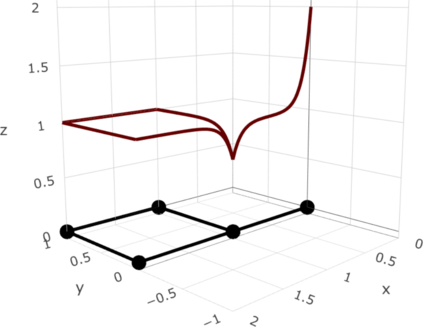
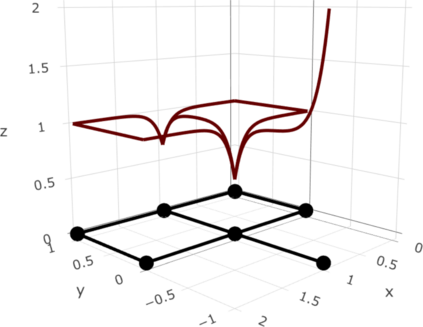
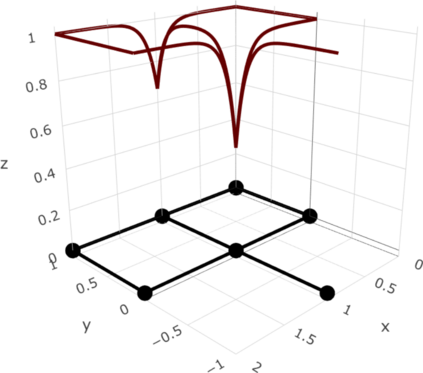
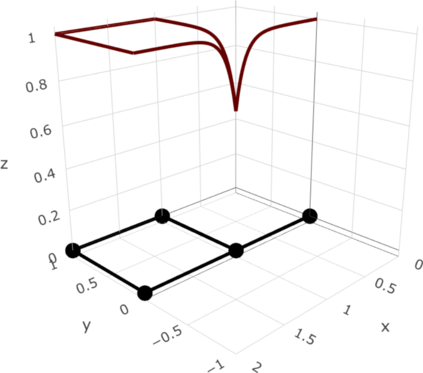
We define a new class of Gaussian processes on compact metric graphs such as street or river networks. The proposed models, the Whittle-Mat\'ern fields, are defined via a fractional stochastic partial differential equation on the compact metric graph and are a natural extension of Gaussian fields with Mat\'ern covariance functions on Euclidean domains to the non-Euclidean metric graph setting. Existence of the processes, as well as their sample path regularity properties are derived. The model class in particular contains differentiable Gaussian processes. To the best of our knowledge, this is the first construction of a valid differentiable Gaussian field on general compact metric graphs. We then focus on a model subclass which we show contains processes with Markov properties. For this case, we show how to evaluate finite dimensional distributions of the process exactly and computationally efficiently. This facilitates using the proposed models for statistical inference without the need for any approximations. Finally, we derive some of the main statistical properties of the model class, such as consistency of maximum likelihood estimators of model parameters and asymptotic optimality properties of linear prediction based on the model with misspecified parameters.