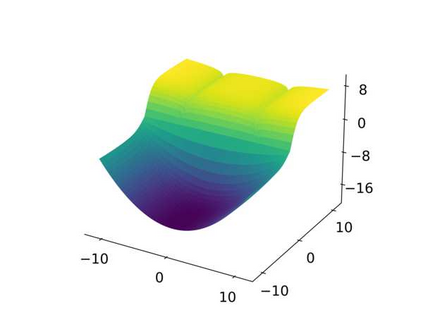
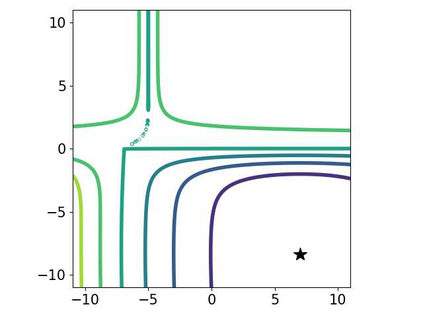
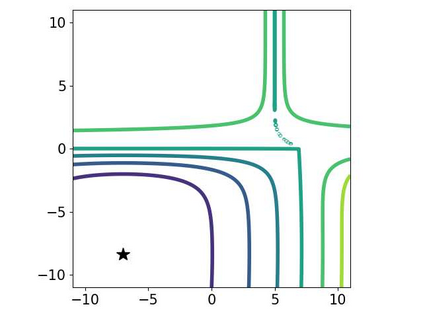
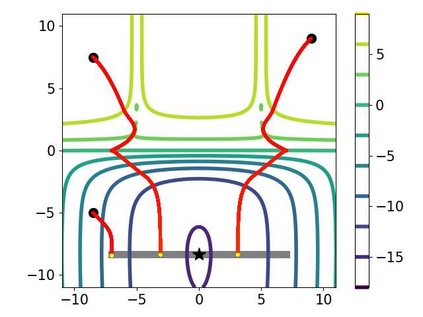
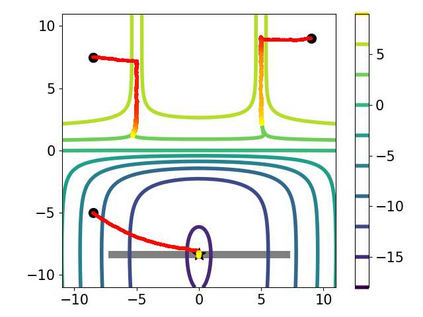
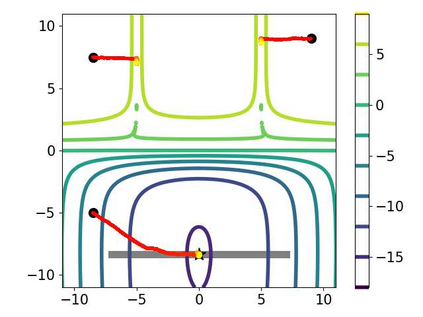
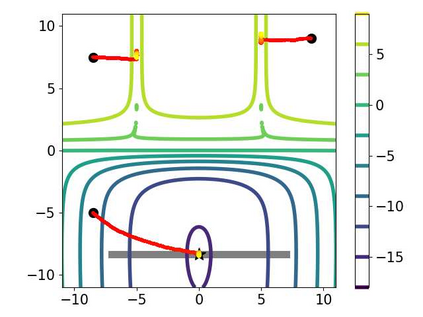
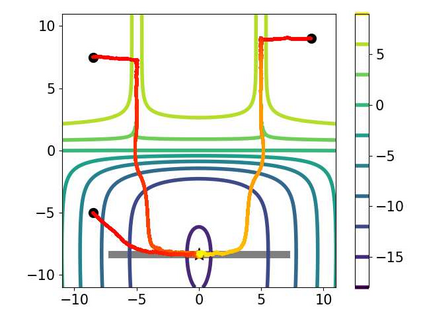
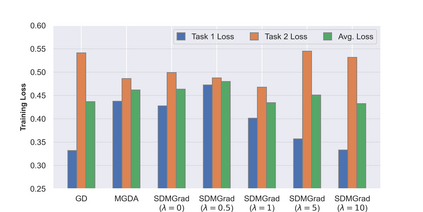
Multi-objective optimization (MOO) has become an influential framework in many machine learning problems with multiple objectives such as learning with multiple criteria and multi-task learning (MTL). In this paper, we propose a new direction-oriented multi-objective problem by regularizing the common descent direction within a neighborhood of a direction that optimizes a linear combination of objectives such as the average loss in MTL. This formulation includes GD and MGDA as special cases, enjoys the direction-oriented benefit as in CAGrad, and facilitates the design of stochastic algorithms. To solve this problem, we propose Stochastic Direction-oriented Multi-objective Gradient descent (SDMGrad) with simple SGD type of updates, and its variant SDMGrad-OS with an efficient objective sampling in the setting where the number of objectives is large. For a constant-level regularization parameter $\lambda$, we show that SDMGrad and SDMGrad-OS provably converge to a Pareto stationary point with improved complexities and milder assumptions. For an increasing $\lambda$, this convergent point reduces to a stationary point of the linear combination of objectives. We demonstrate the superior performance of the proposed methods in a series of tasks on multi-task supervised learning and reinforcement learning. Code is provided at https://github.com/ml-opt-lab/sdmgrad.
翻译:暂无翻译