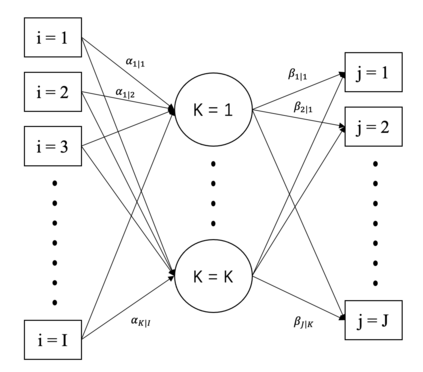
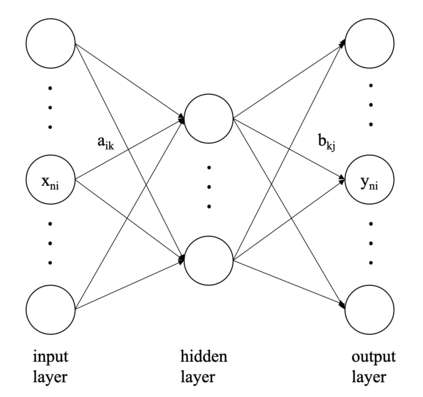
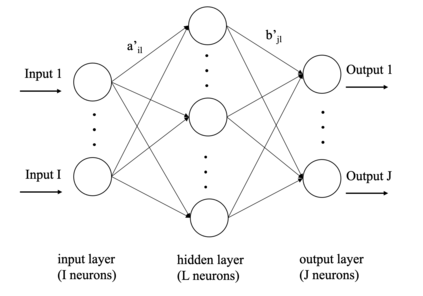
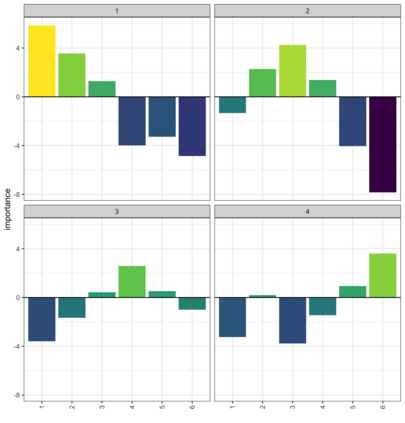
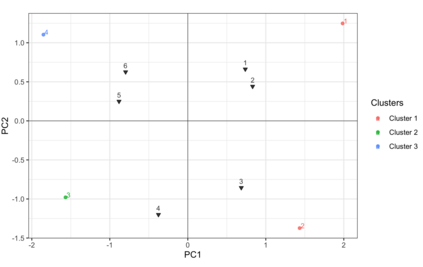
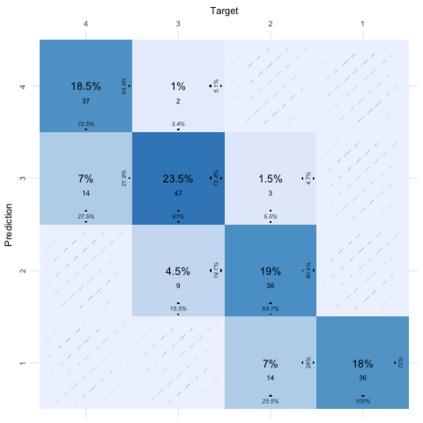
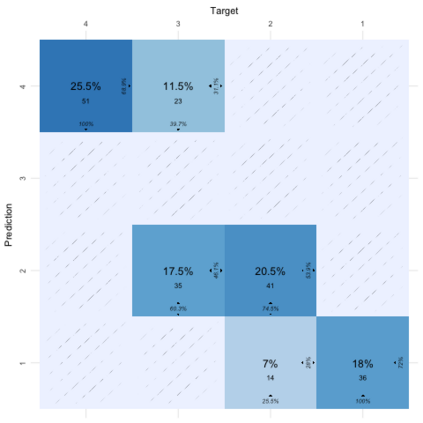
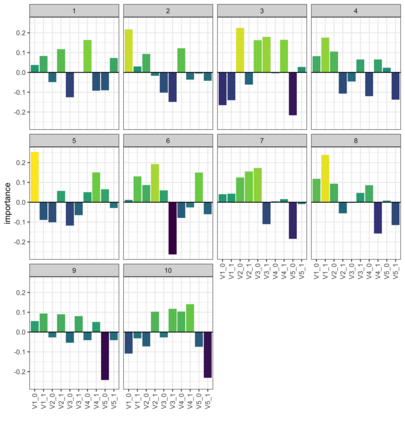
Compositional data are non-negative data collected in a rectangular matrix with a constant row sum. Due to the non-negativity the focus is on conditional proportions that add up to 1 for each row. A row of conditional proportions is called an observed budget. Latent budget analysis (LBA) assumes a mixture of latent budgets that explains the observed budgets. LBA is usually fitted to a contingency table, where the rows are levels of one or more explanatory variables and the columns the levels of a response variable. In prospective studies, there is only knowledge about the explanatory variables of individuals and interest goes out to predicting the response variable. Thus, a form of LBA is needed that has the functionality of prediction. Previous studies proposed a constrained neural network (NN) extension of LBA that was hampered by an unsatisfying prediction ability. Here we propose LBA-NN, a feed forward NN model that yields a similar interpretation to LBA but equips LBA with a better ability of prediction. A stable and plausible interpretation of LBA-NN is obtained through the use of importance plots and table, that show the relative importance of all explanatory variables on the response variable. An LBA-NN-K- means approach that applies K-means clustering on the importance table is used to produce K clusters that are comparable to K latent budgets in LBA. Here we provide different experiments where LBA-NN is implemented and compared with LBA. In our analysis, LBA-NN outperforms LBA in prediction in terms of accuracy, specificity, recall and mean square error. We provide open-source software at GitHub.
翻译:构成数据是用恒定行和总和的矩形矩阵收集的非负数数据。由于非负数,重点是有条件比例,每行加1,每行加1。一个有条件比例的行称为观察到的预算。定期预算分析(LBA)假定的是各种潜在预算的混合体,可以解释观察到的预算。LBA通常安装在应急表上,该表的行与解释变量水平相同,各栏与响应变量水平相仿。在未来的研究中,只了解个人的解释变量,并有兴趣预测反应变量。因此,需要有一种具有预测功能的LBA准确度形式。以前的研究表明,受不满意预测能力的阻碍的LBA神经网络(NN)扩展。我们在这里提议LBA-NN模式,即一个提供与LBA相似的解释变量,我们通过使用重要图和表获得对LBA-NN的中值的中值和中值的LBA(LBA-L)的中值的中值。