The Shapley Value of Classifiers in Ensemble Games

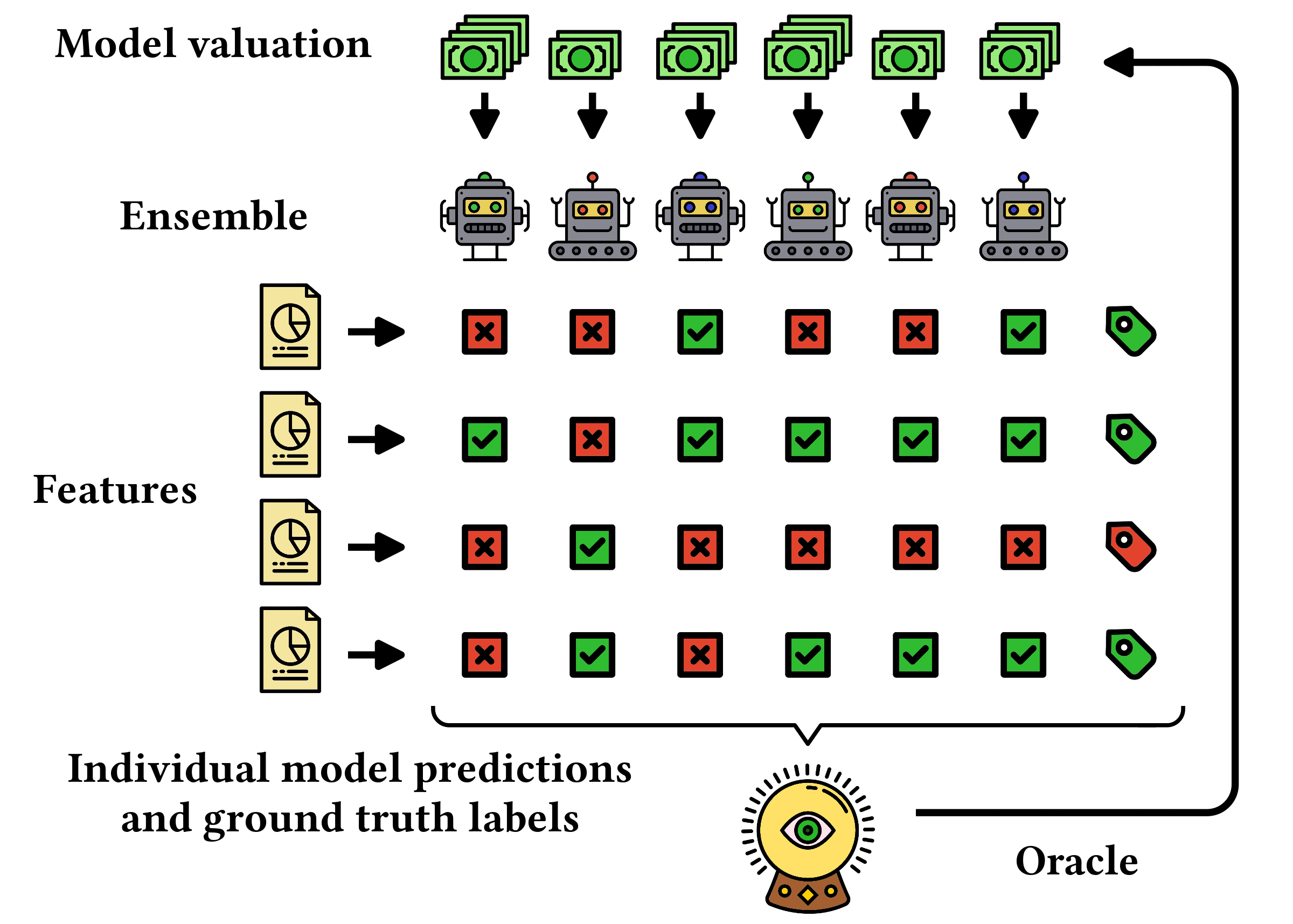
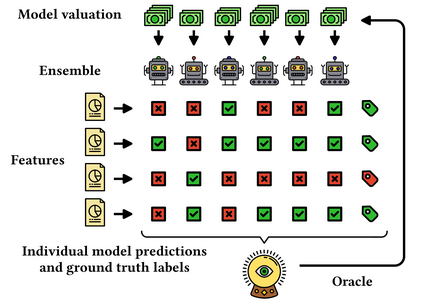
How do we decide the fair value of individual classifiers in an ensemble model? We introduce a new class of transferable utility cooperative games to answer this question. The players in ensemble games are pre-trained binary classifiers that collaborate in an ensemble to correctly label points from a dataset. We design Troupe a scalable algorithm that designates payoffs to individual models based on the Shapley value of those in the ensemble game. We show that the approximate Shapley value of classifiers in these games is an adequate measure for selecting a subgroup of highly predictive models. In addition, we introduce the Shapley entropy a new metric to quantify the heterogeneity of machine learning ensembles when it comes to model quality. We analytically prove that our Shapley value approximation algorithm is accurate and scales to large ensembles and big data. Experimental results on graph classification tasks establish that Troupe gives precise estimates of the Shapley value in ensemble games. We demonstrate that the Shapley value can be used for pruning large ensembles, show that complex classifiers have a prime role in correct and incorrect classification decisions, and provide evidence that adversarial models receive a low valuation.