A Mean-Field Theory for Kernel Alignment with Random Features in Generative Adversarial Networks

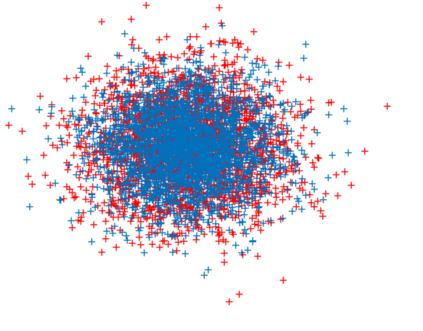
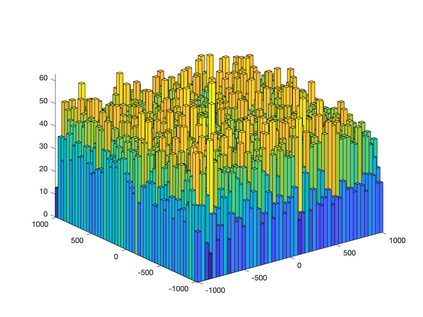
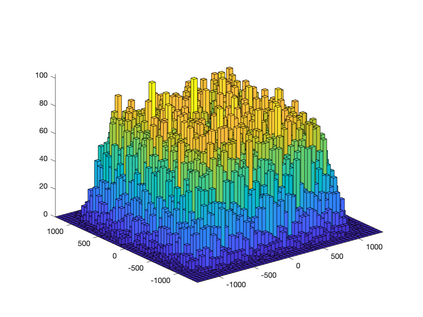
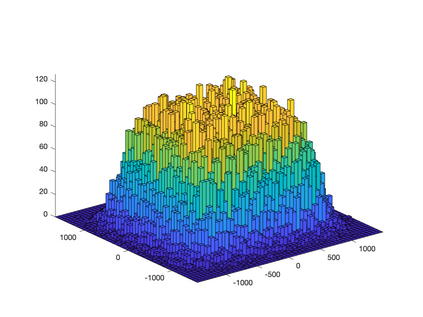
We propose a novel supervised learning method to optimize the kernel in maximum mean discrepancy generative adversarial networks (MMD GANs). Specifically, we characterize a distributionally robust optimization problem to compute a good distribution for the random feature model of Rahimi and Recht to approximate a good kernel function. Due to the fact that the distributional optimization is infinite dimensional, we consider a Monte-Carlo sample average approximation (SAA) to obtain a more tractable finite dimensional optimization problem. We subsequently leverage a particle stochastic gradient descent (SGD) method to solve finite dimensional optimization problems. Based on a mean-field analysis, we then prove that the empirical distribution of the interactive particles system at each iteration of the SGD follows the path of the gradient descent flow on the Wasserstein manifold. We also establish the non-asymptotic consistency of the finite sample estimator. Our empirical evaluation on synthetic data-set as well as MNIST and CIFAR-10 benchmark data-sets indicates that our proposed MMD GAN model with kernel learning indeed attains higher inception scores and lower Fr\`{e}chet inception distances compared to the generative moment matching network (GMMN) and MMD GAN with untrained kernels.