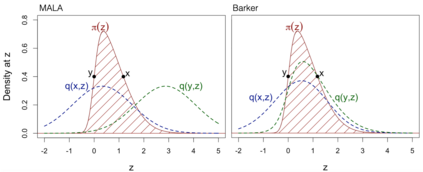
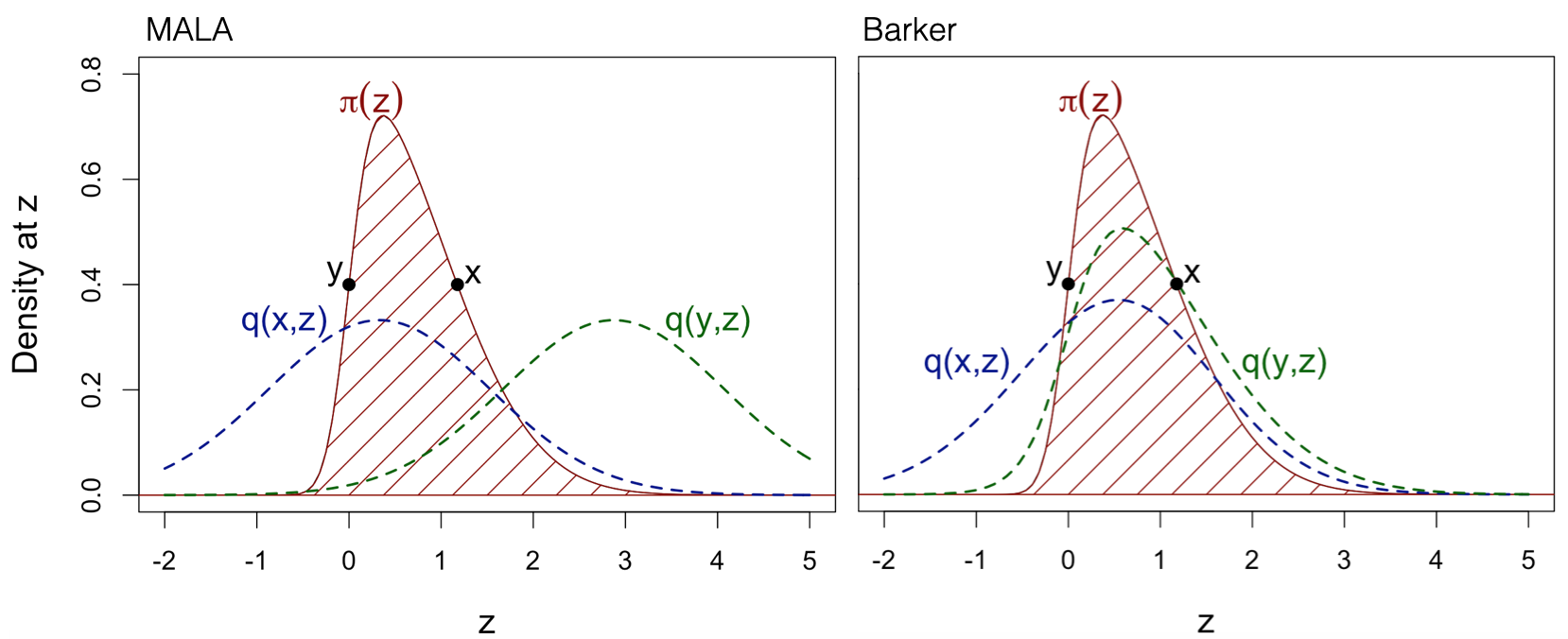
We study a recently introduced gradient-based Markov chain Monte Carlo method based on 'Barker dynamics'. We provide a full derivation of the method from first principles, placing it within a wider class of continuous-time Markov jump processes. We then evaluate the Barker approach numerically on a challenging ill-conditioned logistic regression example with imbalanced data, showing in particular that the algorithm is remarkably robust to irregularity (in this case a high degree of skew) in the target distribution.
翻译:我们根据“ 巴克动力学” 研究了最近推出的基于梯度的马尔科夫连锁蒙特卡洛方法。 我们从最初的原则中充分推导出这种方法, 将其置于更广泛的连续马可夫跳跃过程的类别中。 然后我们用数字来评估巴克尔方法, 以具有不平衡数据的具有挑战性的、条件不完善的后勤回归示例为基础, 尤其表明算法非常稳健, 在目标分布中极不规则( 在本案中, 高度扭曲 ) 。
相关内容
专知会员服务
16+阅读 · 2019年11月30日
专知会员服务
36+阅读 · 2019年10月17日
Arxiv
0+阅读 · 2021年10月25日
Arxiv
0+阅读 · 2021年10月21日
Arxiv
0+阅读 · 2021年10月19日
Arxiv
4+阅读 · 2020年10月20日