多高的AUC才算高？

2016 年 12 月 7 日 ResysChina 张相於

问题的引出

AUC是现在分类模型，特别是二分类模型使用的主要离线评测指标之一。相比于准确率、召回率、F1等指标，AUC有一个独特的优势，就是不关注具体得分，只关注排序结果，这使得它特别适用于排序问题的效果评估，例如推荐排序的评估。

AUC这个指标有两种解释方法，一种是传统的“曲线下面积”解释，另一种是关于排序能力的解释。例如0.7的AUC，其含义可以大概理解为：给定一个正样本和一个负样本，在70%的情况下，模型对正样本的打分高于对负样本的打分。可以看出在这个解释下，我们关心的只有正负样本之间的分数高低，而具体的分值则无关紧要。

我们在各种分享中常常会看到，某大牛的某模型AUC达到了0.xxx，说到此处的大牛脸上一脸的自豪。在崇拜之余，好奇的你一定想过这样一个问题，AUC这个东西，究竟多高算是高？0.7或者0.8的AUC真的很高吗？确实，对于AUC，我们只知道它是介于0和1之间的，对于一个问题，AUC具体能达到多高，好像我们从来不在乎，一般只是用一些“行业经验值”来判断自己模型的AUC够不够高。但是如果不知道理论上AUC能达到多高的话，我们就也无法准确得知当前得到的AUC究竟是高是低。就好像同样是考了90分，在100分满分的制度下和150分满分的制度下，含义是完全不同的。所以，今天我们就来做一番探索，看看对于一个具体问题，AUC理论上究竟能达到多高，以及理论上AUC最高值的高低和哪些因素有关。

理论最高AUC

为了便于清晰地讨论，我们先明确一下讨论的具体概念是什么。我们在这里关心的概念是一个数据集的理论最高AUC（以下简称Max AUC）。这个“理论最高”指的是什么呢？具体来说，指的就是如果我们拥有“上帝视角”，也就是一个超级NB的分类器——这个分类器知道每条样本的真实分类概率——在这个数据集上能够达到的AUC。等等，难道拥有了上帝视角之后，AUC还不就是1了么？还真不一定，我们看一下下面这个小例子。

在这个例子中，我们一共有三条样本，每个样本有两个特征，其中“预测分类概率”指的是样本属于类别1的概率。这个数据集的具体情况如下：

样本ID	特征1	特征2	真实标签	预测分类概率
1	1	1	0	0.5
2	1	1	1	0.5
3	1	0	0	0

请注意最后一列“预测分类概率”，这一列指的是我们的“上帝视角分类器”（下面简为GC：God Classifier）给出的分类概率，所谓的GC，其实就是一个记忆力超群的超级过拟合的分类器。可以看到对于3号样本，GC正确地给出了0的预测概率，但是对于1号和2号样本，即使是GC也只能给出0.5的分类概率，为什么呢？原因就是这两条样本的特征取值完全相同，但是标签不相同，所以GC在这上面犯了“必须犯的错误”，所谓必须犯的错误，也就是无法避免的错误，因为你无法从特征中无法区分这两条样本，基于最大熵原理，给出同等概率是最好的选择。犯了这个错误之后，AUC自然也就不可能是完美的1了。

所以我们看到，开了上帝视角也不能随心所欲地操纵AUC，那么开了上帝视角之后，AUC究竟最高能达到多高呢？这就是本文要讨论的问题。

影响Max AUC的因素

上面的讨论不但给出了我们要讨论的核心概念——Max AUC，同时也通过一个例子给出了影响这个概念的主要因素：样本的不确定性。所谓样本的不确定性，指的是对于完全相同的样本，也就是特征取值完全相同的样本，其对应的标签是否存在不确定性，例如上文中的例子，1号样本和2号样本对应的特征取值就完全相同，但是标签却不相同，因此就引入了不确定性，而这个不确定性的程度的大小，也就决定了Max AUC的取值。而如果样本中没有任何的不确定性，则每条样本的标签就是唯一确定的，我们的GC就可以记住它的标签，从而给出正确的预测。

为了验证这个猜想，并且量化地查看不同程度的不确定性对于Max AUC的影响，我写了一个模拟程序来生成一组数据（文末有这份代码的github地址），并在这组数据上计算了Max AUC和样本不确定性的关系。

实验的具体方法如下：

对于不同程度的不确定性：

根据该不确定性，生成测试的样本数据，并使用上帝视角给出预测的分类概率。
计算该数据集上的AUC。

具体来说，我们用随机数的方法来模拟不确定性：在生成新样本时，如果根据该随机数，来选择是否使用新的特征取值，如果使用旧的特征取值，则再随机给一个标签，具体代码如下：

if random.random() > dup_ratio:

feature_id += 1

label = random.randint(0, 1)

其中dup_ratio这个变量用来控制重复生成样本的几率，也就是不确定性。这里注意到我们仅使用一个id来代表一个特征（feature_id），这是因为在我们的问题中，我们只关心特征取值是否相同，而不关心具体的取值，毕竟我们不会训练一个具体的分类器，而是在使用“上帝视角”的分类器。所以在这种场景下，只需要一个id来区分表示不同取值的特征即可。

在生成了“特征取值+标签”的样本后，我们为每条样本计算了GC给出的分类概率，方法也很简单，就是使用最大熵原理给不确定性样本赋予等概率值。

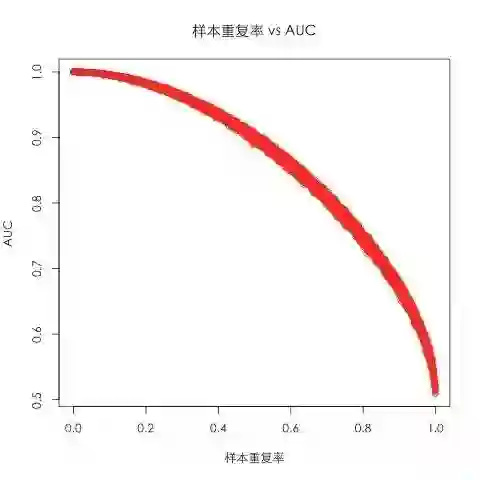
在这个实验设定下，越高的样本重复率（dup_ratio），代表了数据集中越高的不确定性，因为会有越多的特征相同的样本拥有不同的label，那么按照我们的猜想，对应的Max AUC应该也会越低。那么这两者具体的关系如何呢？我们将样本重复率作为横轴，Max AUC作为纵轴，便可得到如下的图（使用R绘图所得）：

上图在计算每次Max AUC的时候（也就是图上的每一个点）使用了一万个数据点。可以看出随着样本重复率的升高，Max AUC确实在不断降低，最终降到0.5——AUC的最低取值。

贝叶斯错误率

上面我们用简单的实验揭示了Max AUC和样本中不确定性之间的关系，这种样本中的不确定性，是“上帝视角分类器”也无能为力的，如果从优化问题的角度来看的话，属于不可优化的部分。说到这里，统计学中还有另外一个概念，和“不可优化”这个思想不谋而合，那就是贝叶斯错误率（Bayes Error Rate，以下简称为BER）。BER的具体定义大家可以去查看Wikipedia或者其他资料，如果用一句话来概括其思想的话，可以这么说：BER指的是任意一个分类器在一个数据集上能取得的最低的错误率。而这个错误率，则对应着数据中的不可约错误（irreducible error），也就是我们刚刚说到的“上帝视角也无法解决的错误”，“必须犯的错误”。

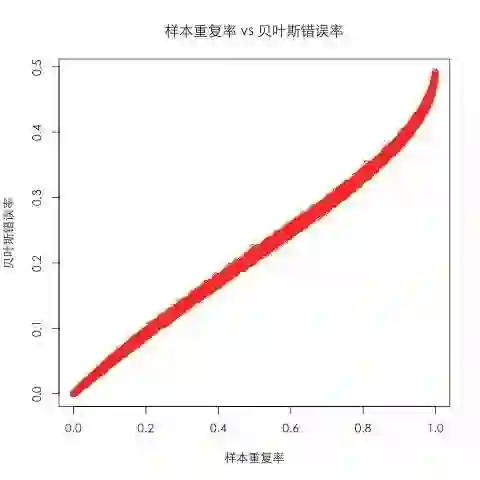
通过分析BER的定义，我们可以知道，所谓的“不可约错误”只会在样本中出现不确定性的时候发生——这和我们刚刚模拟数据使用的假设是相同的，于是我们使用刚刚的数据计算出不同样本重复率对应的BER，其图像如下：

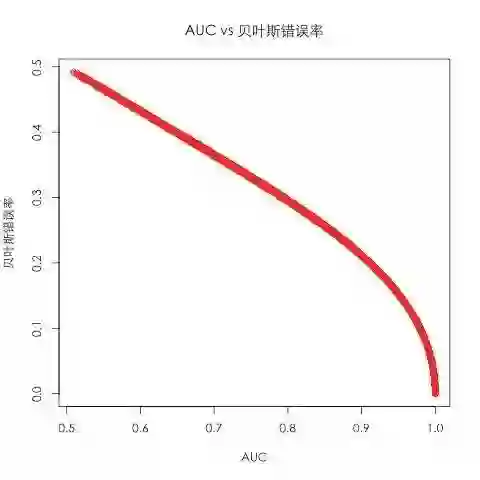
可以看出，样本重复率和BER有着明确的近乎线性的关系（，而我们在上一节中看到样本重复率和Max AUC也有着明确的相关性，所以很自然地，Max AUC和BER之间也存在很强的相关性，如下图所示：

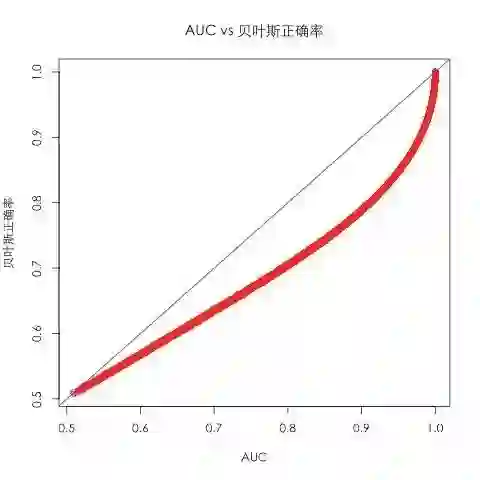
因为BER是一种错误指标，其取值是越低越好，和AUC相反，所以我们将BER换算为1-BER，又可得到如下图像：

图中蓝色的线是y=x的直线。其中“贝叶斯正确率”是为了和“贝叶斯错误率”相对比而造出来的概念，其取值等于1-BER，统计学中并无此概念。可以看出Max AUC和BER之间有着强烈的正相关关系。

真实数据集结果

上面我们通过实验探索了Max AUC以及影响它的因素，并探索了它和贝叶斯错误率之间的关系，那么在真实数据中这种关系是否真实存在呢？为了验证这一点，我从我们工作中用到的两个数据集中计算了对应的AUC和BER，其中AUC包括Max AUC和真实模型给出的真实AUC。两个数据集和模型的表现如下：

数据集/指标	真实AUC	Max AUC	BER
数据集1	0.753	0.971	0.033
数据集2	0.744	0.999	0.009

可以看出，在这两个数据集上来看，Max AUC和BER确实存在着正相关的关系，但是如果拿着0.033的BER到我们的模拟数据中去找的话，对应的Max AUC是0.997，并不是实际中的0.971。造成这两者之间的差异的原因之一，是因为我们在生成模拟数据的生成重复样本步骤中，使用了等概率来产生0和1两种标签，而真实数据中可能并不是这样，换句话说，这两份数据在具体的不确定性上并不完全相同，有兴趣的同学可以进一步探索不通的不确定性对于两者关系的影响。

从上面的数据，我们还可以看出一点，那就是Max AUC和真实模型AUC的高低并没有正相关的关系，这是因为这两份数据上模型的特征表达能力各不相同，数据集1上的特征表现出了对标签的更好的可区分性。

启示

通过上面简单的分析，我们可以得到以下一些启示：

Max AUC的高低只和特征取值的多样性有关。其实不只是Max AUC，在真实问题中使用更多好的特征也会提高AUC（起码是训练集AUC），本质上是因为更多的特征可以组合出更多的特征取值来，从而提高特征的区分能力。关于这部分更详细的理论解释，以及其与VC Dimension的关系，有兴趣的同学可以参考公开课<Learningfrom Data>的前几章节(http://work.caltech.edu/telecourse.html)。同时这也是一门非常好的机器学习理论入门课程，推荐给有兴趣的同学。
贝叶斯错误率与Max AUC有着密切的关系。由于这两个指标衡量的都是数据集中不可约错误（irreducible error），所以他们在数值上表现出了很强的相关性。但是我们从两个实际例子中也可以看到，具体的关系还和数据中的不确定性相关。
更高的Max AUC并不代表更高的真实模型AUC。虽然更高的Max AUC代表了更多的特征取值可能性，但是影响真实AUC的，还有特征的具体区分度，也就是泛化能力。

总结

本文从“AUC究竟能有多高”这个问题出发，简单探讨了AUC和贝叶斯错误率这两个概念，以及他们之间的关系，并简单分析了Max AUC和真实AUC之间的一些关系。

由于时间匆忙和能力所限，本文并没有给出这两者之间理论关系的分析，做的实验也比较简单，所以充其量只是一块“砖”，希望可以引出更多的“玉”。本文使用的实验代码可在这里找到：https://github.com/ruczhangxy/bayes_error_rate_vs_auc。欢迎有兴趣的同学拿去折腾。

本文作者：

张相於，现任58集团转转事业部算法架构师，负责转转的搜索&推荐系统。曾任当当网推荐系统开发经理，多年来主要从事推荐系统以及机器学习相关工作，也做过反垃圾、反作弊相关工作，并热衷于探索大数据技术&机器学习技术在其他领域的应用实践。

★ 猜你喜欢：「机器学习系统丛林迷路指南」

广告时间：

转转推荐搜索团队诚招靠谱算法工程师：转转是58集团旗下的专业二手交易平台，现在正在高速发展中，拥有干净的海量数据，独一无二的挑战性问题，更拥有广阔的发展空间和一群靠谱的小伙伴，无论你是希望快速成长还是希望建功立业，这里都是你最好的选择。有意者请发简历到zhangxiangyu01@58ganji.com。