Disentangling Generative Factors of Physical Fields Using Variational Autoencoders

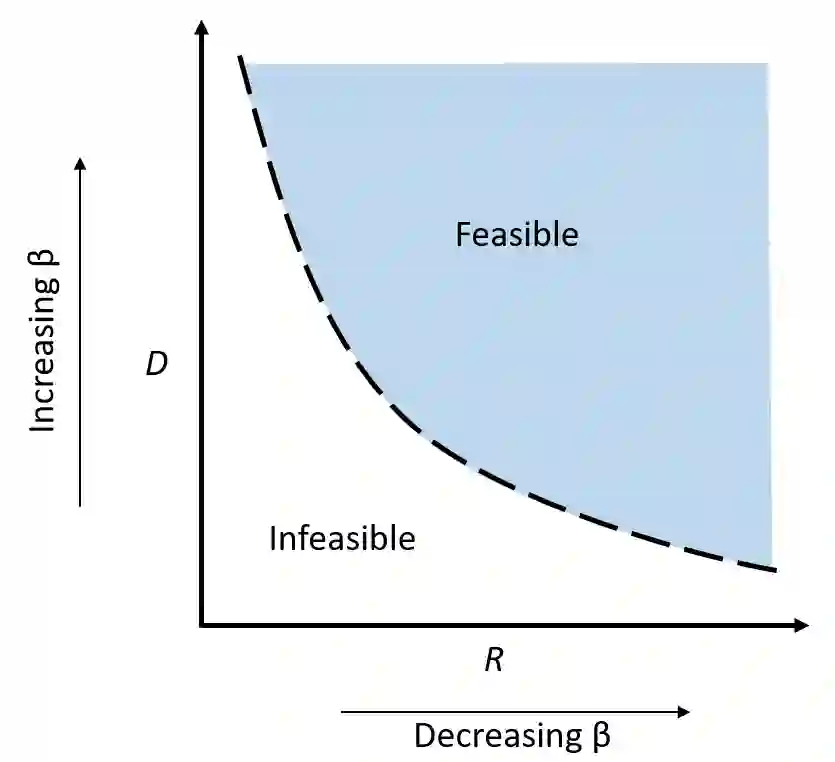
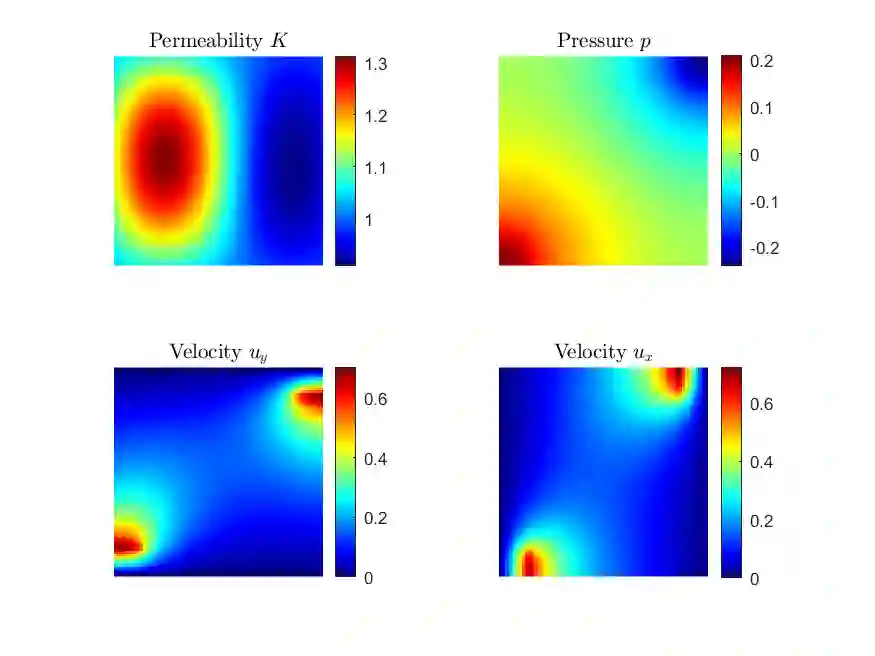
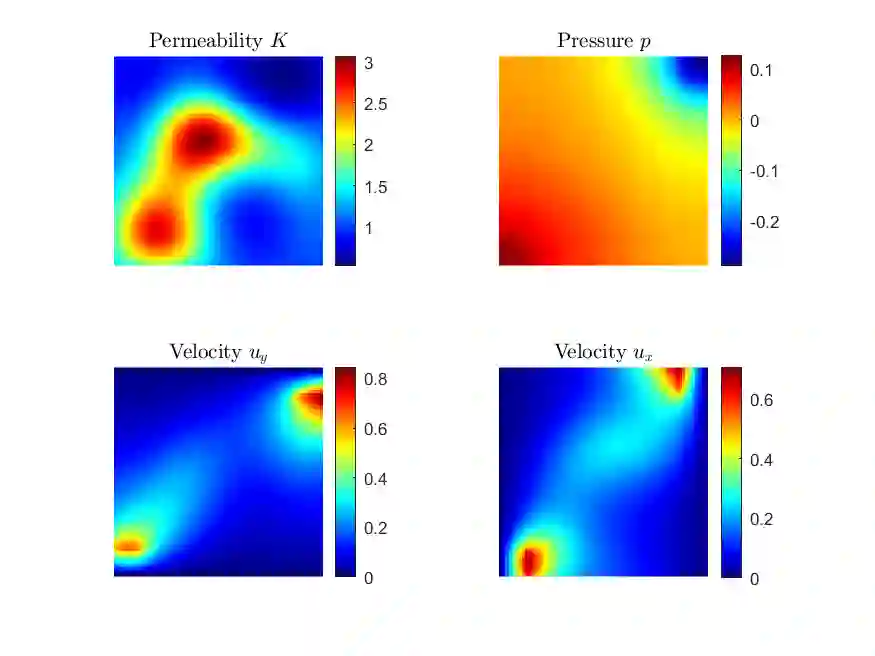
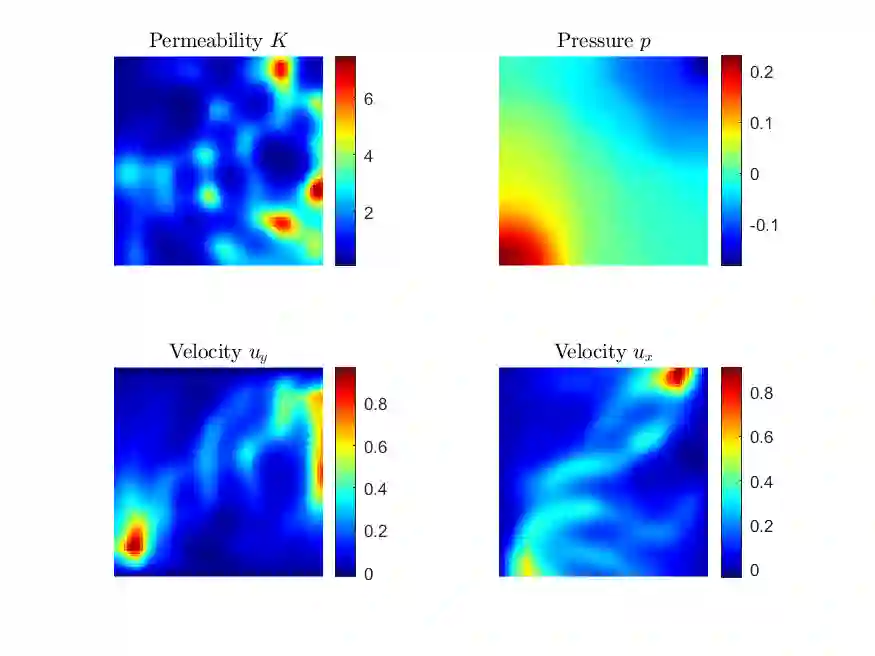
The ability to extract generative parameters from high-dimensional fields of data in an unsupervised manner is a highly desirable yet unrealized goal in computational physics. This work explores the use of variational autoencoders (VAEs) for non-linear dimension reduction with the specific aim of {\em disentangling} the low-dimensional latent variables to identify independent physical parameters that generated the data. A disentangled decomposition is interpretable, and can be transferred to a variety of tasks including generative modeling, design optimization, and probabilistic reduced order modelling. A major emphasis of this work is to characterize disentanglement using VAEs while minimally modifying the classic VAE loss function (i.e. the Evidence Lower Bound) to maintain high reconstruction accuracy. The loss landscape is characterized by over-regularized local minima which surround desirable solutions. We illustrate comparisons between disentangled and entangled representations by juxtaposing learned latent distributions and the true generative factors in a model porous flow problem. Hierarchical priors are shown to facilitate the learning of disentangled representations. The regularization loss is unaffected by latent rotation when training with rotationally-invariant priors, and thus learning non-rotationally-invariant priors aids in capturing the properties of generative factors, improving disentanglement. Finally, it is shown that semi-supervised learning - accomplished by labeling a small number of samples ($O(1\%)$) - results in accurate disentangled latent representations that can be consistently learned.