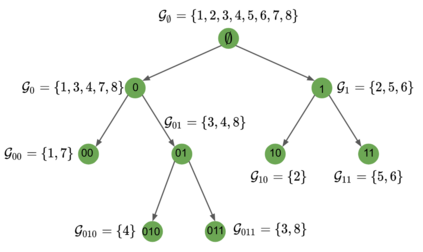
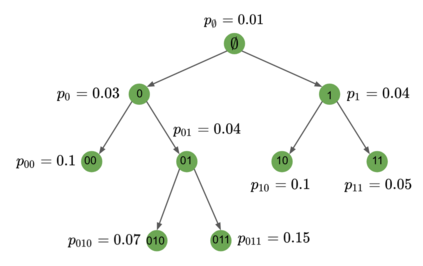
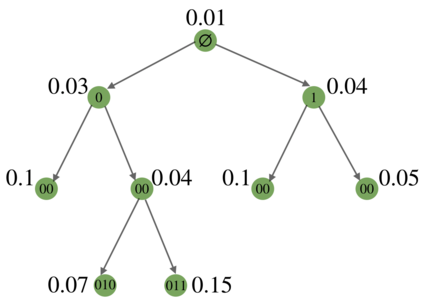
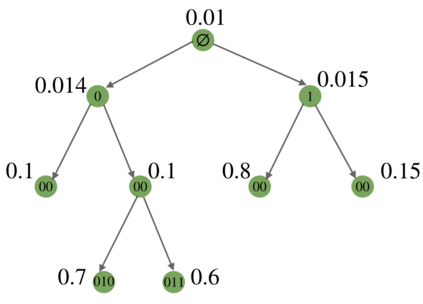
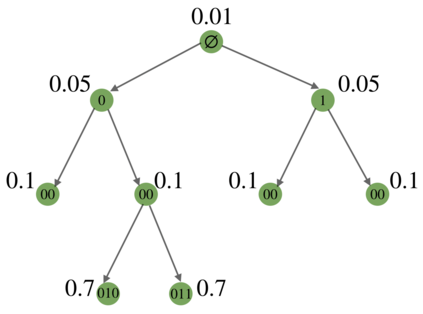
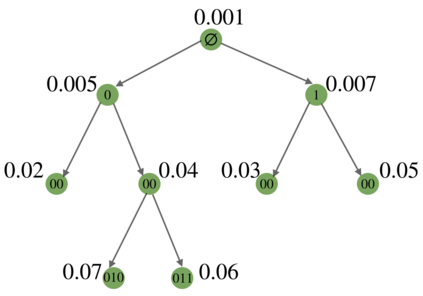
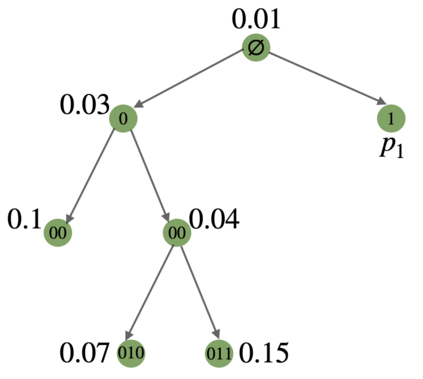
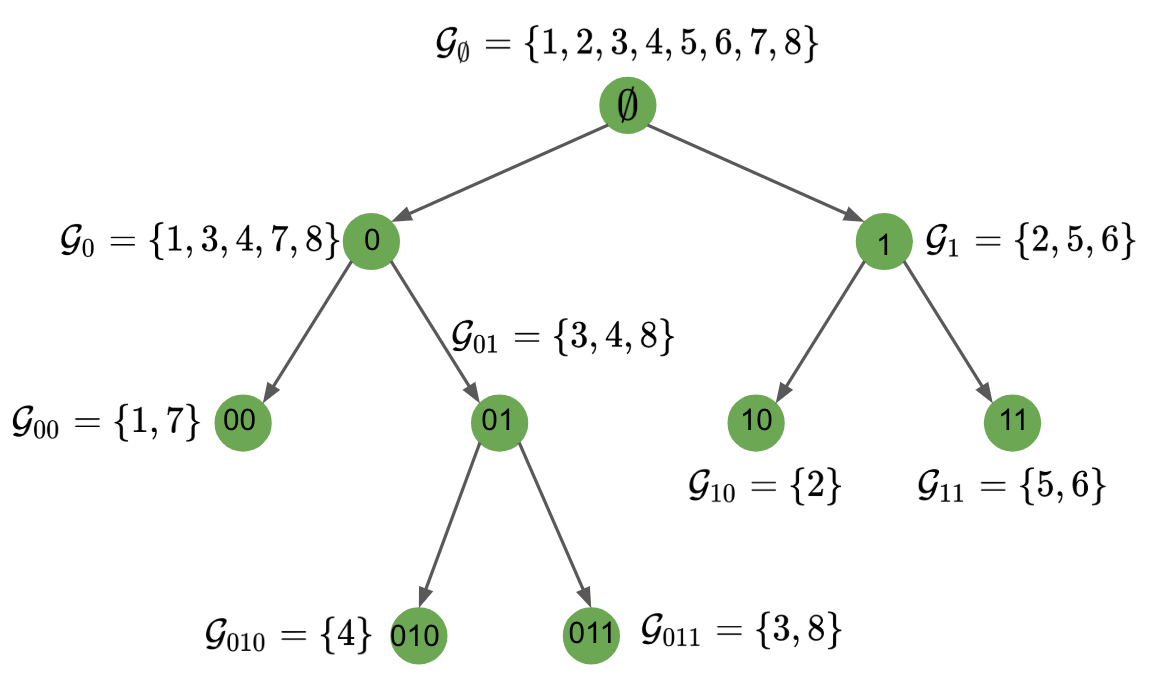
We study the hierarchy of communities in real-world networks under a generic stochastic block model, in which the connection probabilities are structured in a binary tree. Under such model, a standard recursive bi-partitioning algorithm is dividing the network into two communities based on the Fiedler vector of the unnormalized graph Laplacian and repeating the split until a stopping rule indicates no further community structures. We prove the strong consistency of this method under a wide range of model parameters, which include sparse networks with node degrees as small as $O(\log n)$. In addition, unlike most of existing work, our theory covers multiscale networks where the connection probabilities may differ by orders of magnitude, which comprise an important class of models that are practically relevant but technically challenging to deal with. Finally we demonstrate the performance of our algorithm on synthetic data and real-world examples.
翻译:我们在一个通用的随机区块模型下研究现实世界网络中的社区等级,其中连接概率在一棵二树上结构。在这种模型下,标准的递归双分算法将网络分成两个社区,以非正常的图解的Fiedler矢量为基础,重复这一划分,直到停止规则表明没有进一步的社区结构。我们证明这种方法在一系列广泛的模型参数下非常一致,其中包括小于O(\log n)美元的节点的稀少网络。此外,与大多数现有工作不同,我们的理论涵盖多尺度网络,其中连接概率可能因数量大小而不同,这构成了一个重要的模型类别,实际上具有相关性,但在技术上具有挑战性。最后,我们展示了我们在合成数据和现实世界实例方面的算法表现。