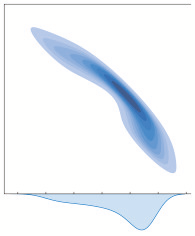
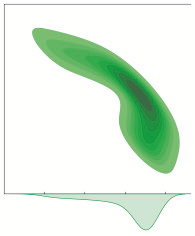
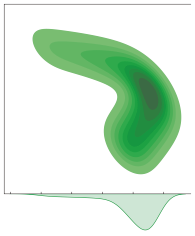
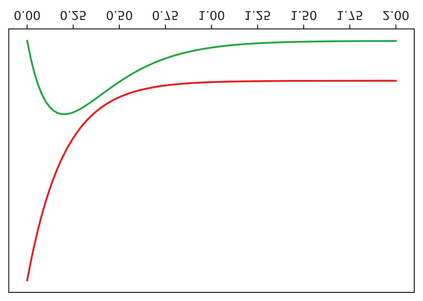
Embedding knowledge graphs (KGs) for multi-hop logical reasoning is a challenging problem due to massive and complicated structures in many KGs. Recently, many promising works projected entities and queries into a geometric space to efficiently find answers. However, it remains challenging to model the negation and union operator. The negation operator has no strict boundaries, which generates overlapped embeddings and leads to obtaining ambiguous answers. An additional limitation is that the union operator is non-closure, which undermines the model to handle a series of union operators. To address these problems, we propose a novel probabilistic embedding model, namely Gamma Embeddings (GammaE), for encoding entities and queries to answer different types of FOL queries on KGs. We utilize the linear property and strong boundary support of the Gamma distribution to capture more features of entities and queries, which dramatically reduces model uncertainty. Furthermore, GammaE implements the Gamma mixture method to design the closed union operator. The performance of GammaE is validated on three large logical query datasets. Experimental results show that GammaE significantly outperforms state-of-the-art models on public benchmarks.
翻译:用于多点逻辑推理的嵌入式知识图表(KGs)是一个挑战性的问题,因为许多KGs中的结构庞大而复杂。最近,许多有前途的工程预测实体和查询进入几何空间以有效找到答案。然而,对否定和工会经营者来说,仍然具有挑战性。否定操作者没有严格的界限,这会造成嵌入重叠,并导致获得模糊的答案。另一个限制是,工会经营者是非封闭型的,这破坏了处理一系列工会经营者的模式。为了解决这些问题,我们提议了一个新型的概率嵌入模型,即伽玛嵌入式(Gamma Empeddings),用于编码实体和查询,以解答关于KGGG的不同类型的FOL查询。我们利用伽玛分布的线性属性和强有力的边界支持来捕捉更多的实体特征和查询,这大大降低了模型的不确定性。此外,伽玛公司采用伽玛混合法来设计封闭式工会经营者。Gammae的性能在三大逻辑查询数据集中得到验证。实验结果显示,伽玛公司在公共基准上明显超越了状态。