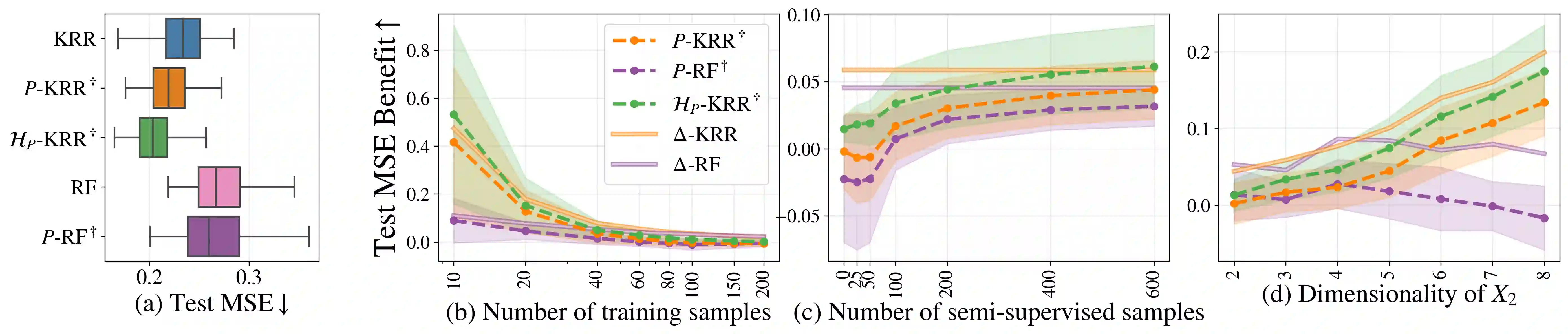
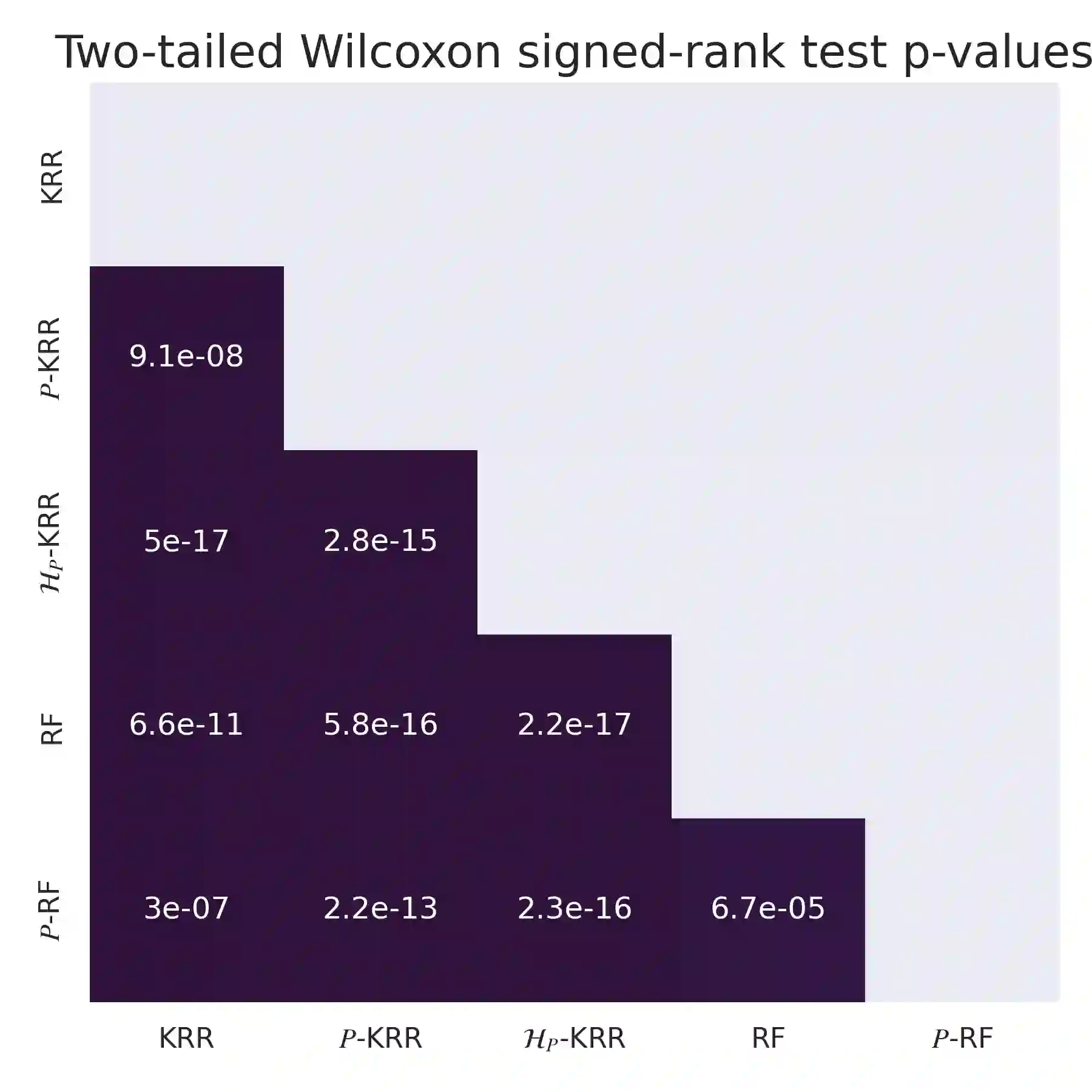
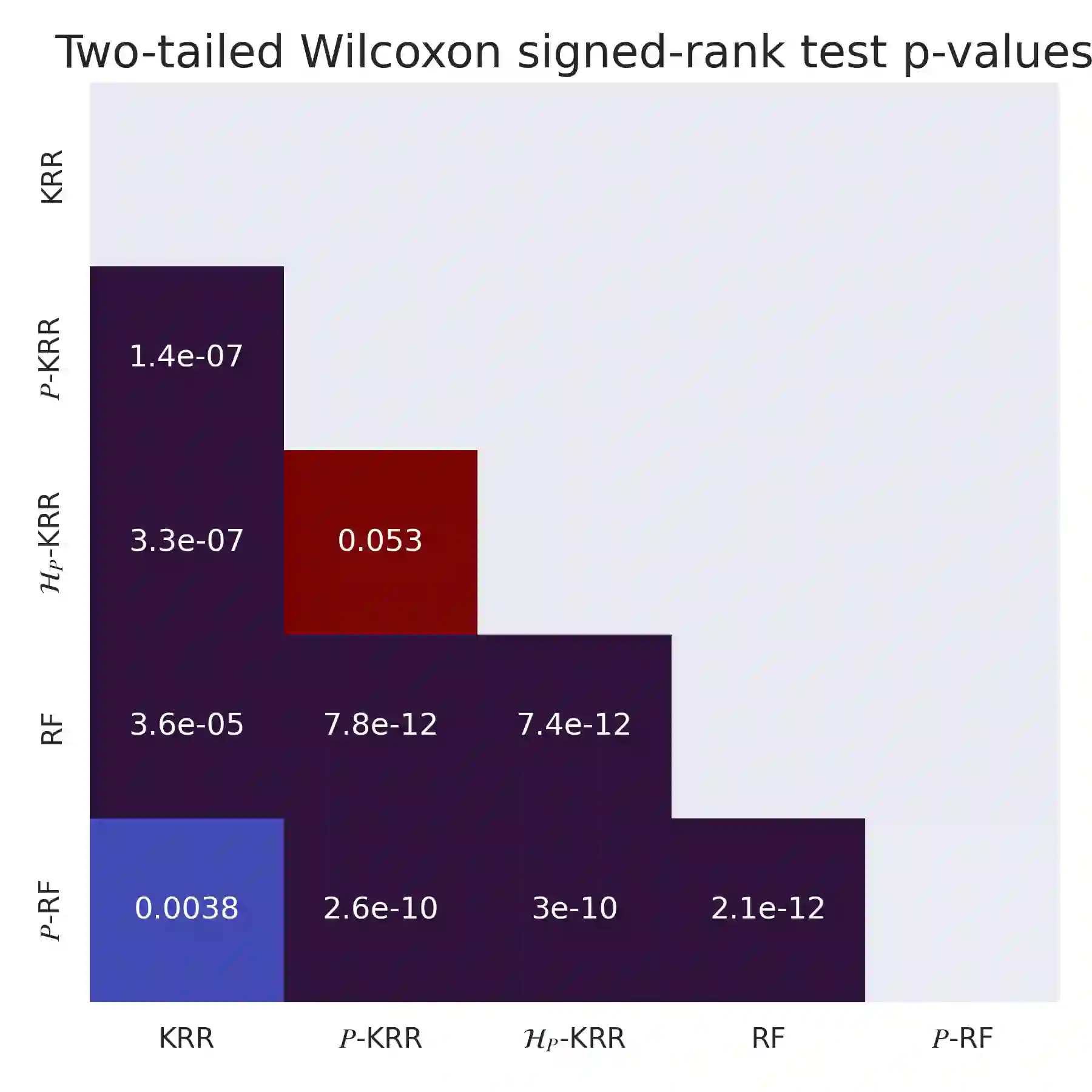
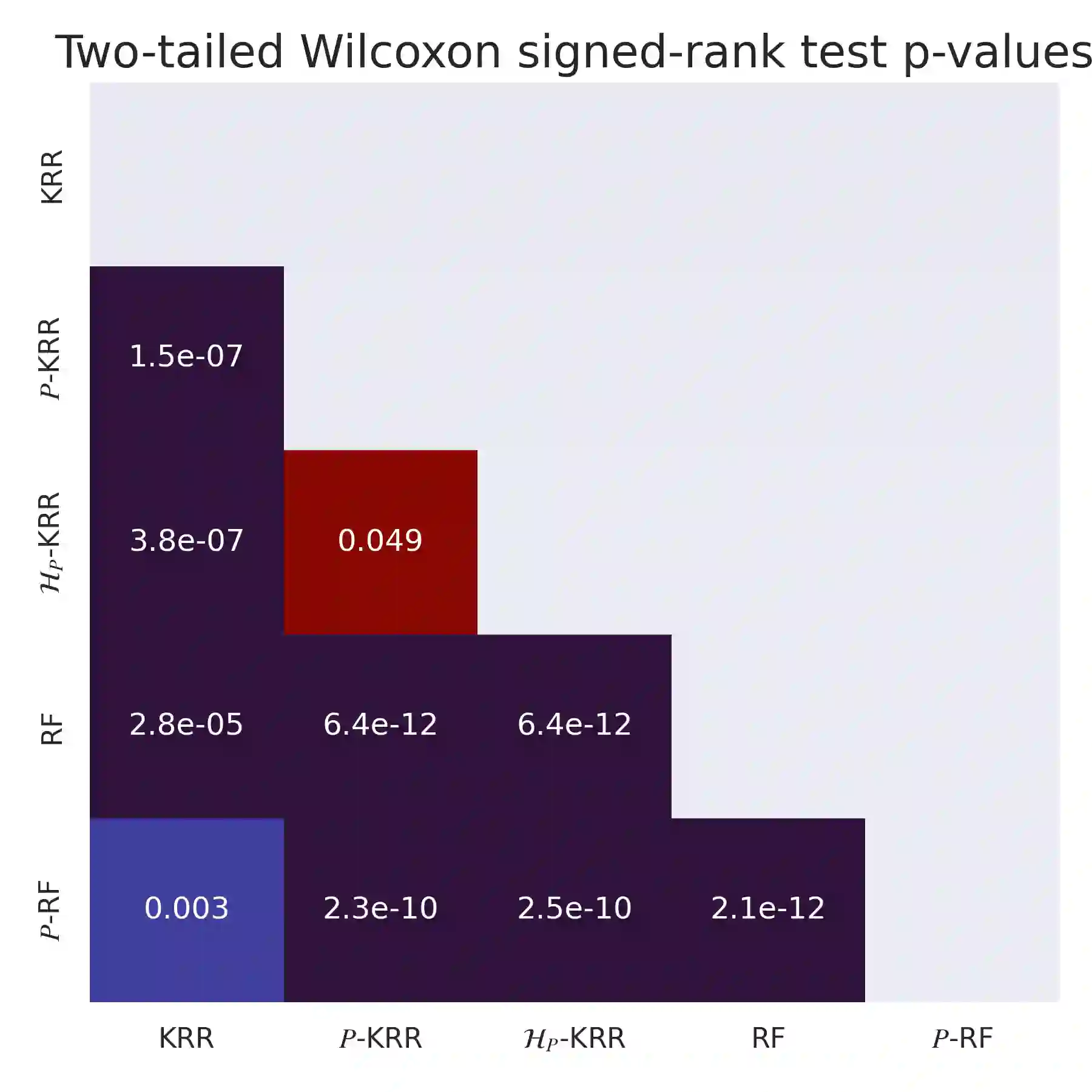
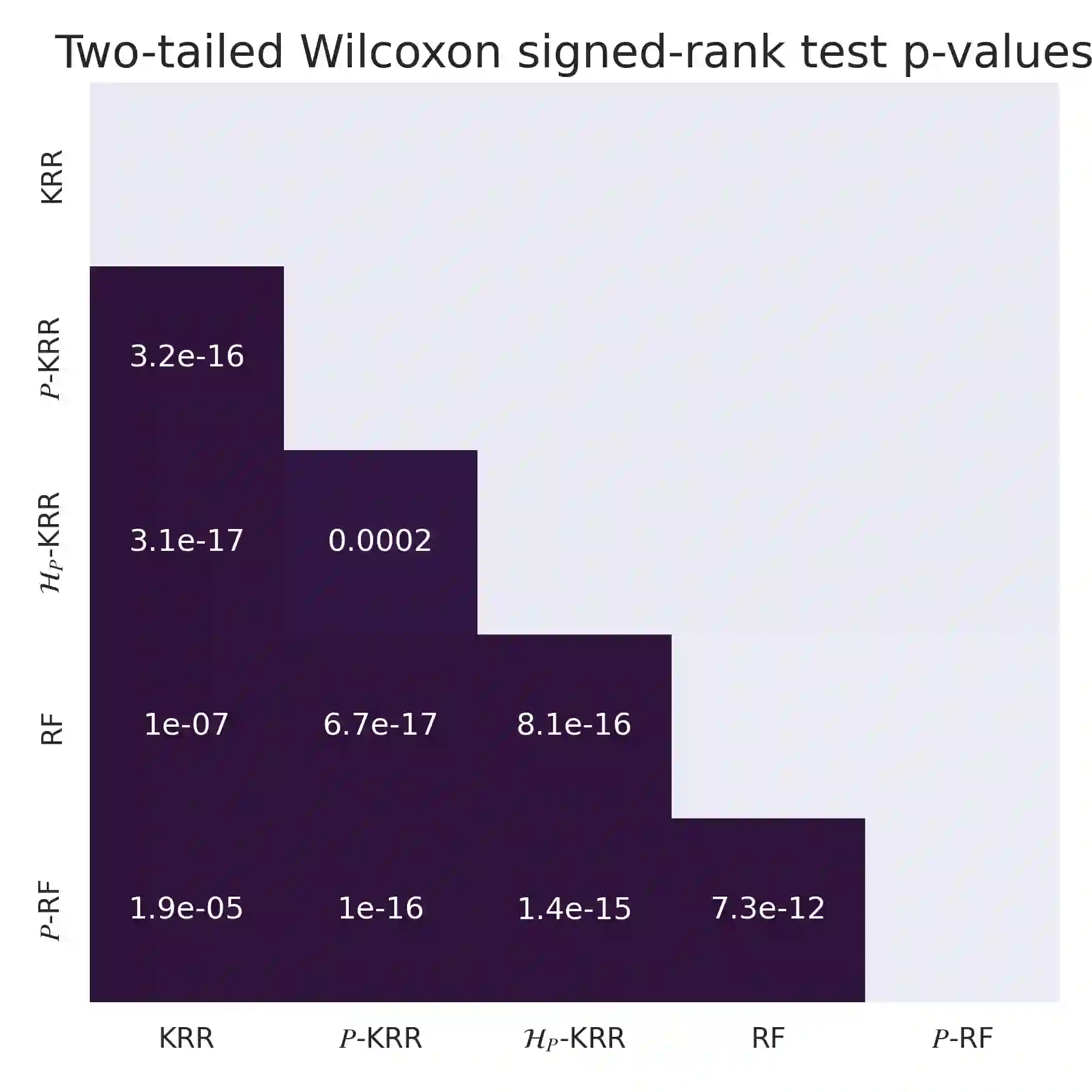
A directed acyclic graph (DAG) provides valuable prior knowledge that is often discarded in regression tasks in machine learning. We show that the independences arising from the presence of collider structures in DAGs provide meaningful inductive biases, which constrain the regression hypothesis space and improve predictive performance. We introduce collider regression, a framework to incorporate probabilistic causal knowledge from a collider in a regression problem. When the hypothesis space is a reproducing kernel Hilbert space, we prove a strictly positive generalisation benefit under mild assumptions and provide closed-form estimators of the empirical risk minimiser. Experiments on synthetic and climate model data demonstrate performance gains of the proposed methodology.
翻译:定向循环图(DAG)提供了宝贵的先前知识,这些知识常常被机器学习中的回归任务所抛弃。我们表明,由于DAG中存在对撞结构而产生的独立性提供了有意义的感应偏差,制约了回归假设空间并改进了预测性性能。我们引入了对撞回归框架,将串撞器的概率性因果知识纳入回归问题。当假设空间是复制内核希尔伯特空间时,我们证明在轻度假设下是一种绝对积极的概括效益,并提供实证风险最小值的封闭式估计。关于合成和气候模型数据的实验显示了拟议方法的绩效收益。