The Fragility of Optimized Bandit Algorithms

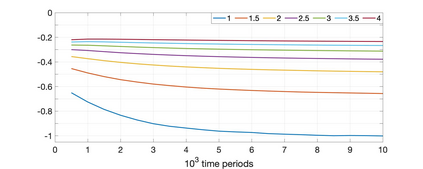
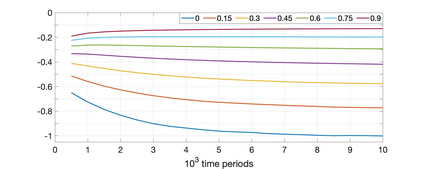
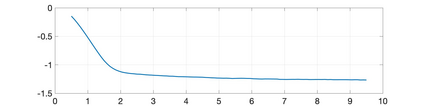
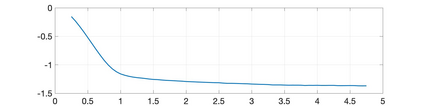
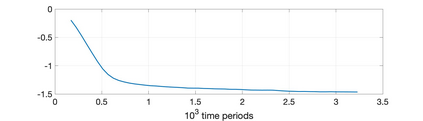
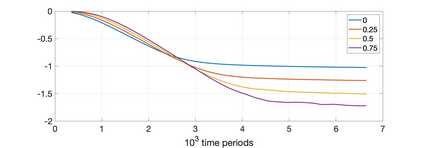
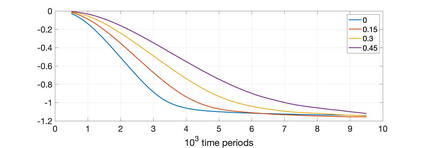
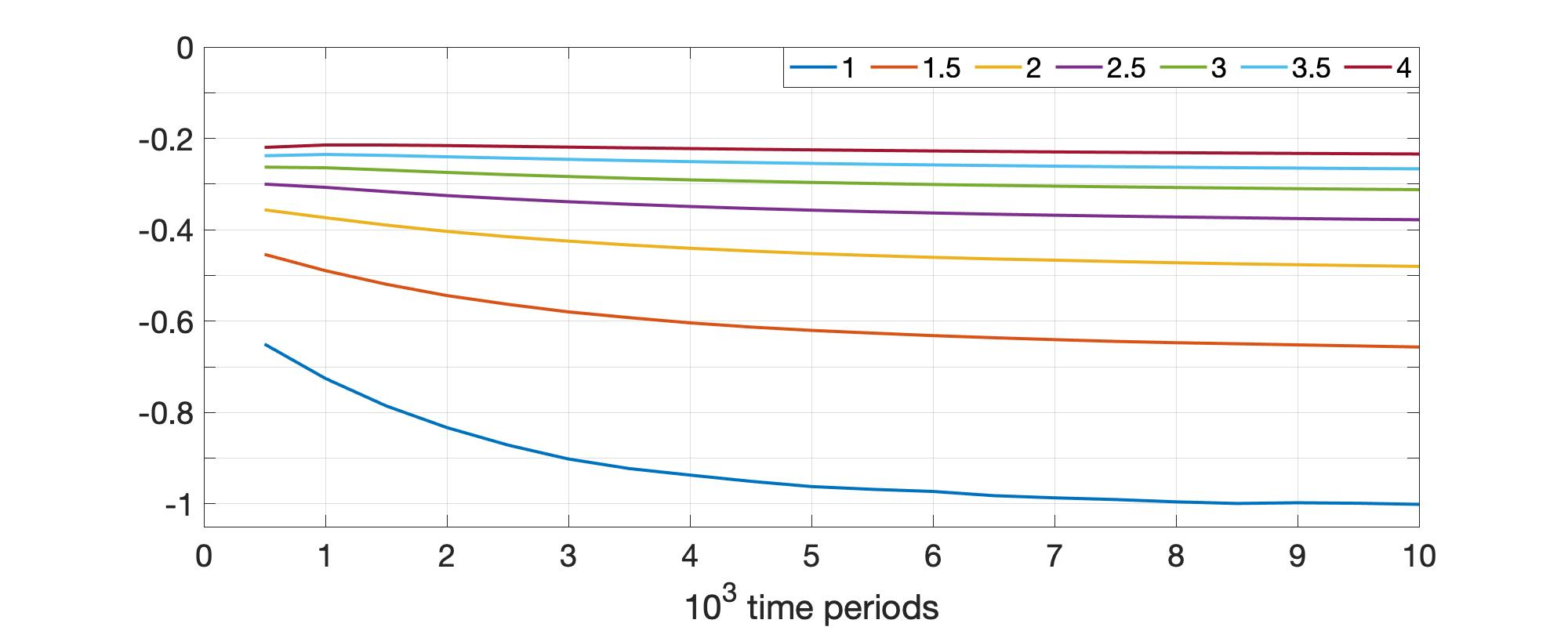
Much of the literature on optimal design of bandit algorithms is based on minimization of expected regret. It is well known that designs that are optimal over certain exponential families can achieve expected regret that grows logarithmically in the number of arm plays, at a rate governed by the Lai-Robbins lower bound. In this paper, we show that when one uses such optimized designs, the regret distribution of the associated algorithms necessarily has a very heavy tail, specifically, that of a truncated Cauchy distribution. Furthermore, for $p>1$, the $p$'th moment of the regret distribution grows much faster than poly-logarithmically, in particular as a power of the total number of arm plays. We show that optimized UCB bandit designs are also fragile in an additional sense, namely when the problem is even slightly mis-specified, the regret can grow much faster than the conventional theory suggests. Our arguments are based on standard change-of-measure ideas, and indicate that the most likely way that regret becomes larger than expected is when the optimal arm returns below-average rewards in the first few arm plays, thereby causing the algorithm to believe that the arm is sub-optimal. To alleviate the fragility issues exposed, we show that UCB algorithms can be modified so as to ensure a desired degree of robustness to mis-specification. In doing so, we also provide a sharp trade-off between the amount of UCB exploration and the tail exponent of the resulting regret distribution.