Adaptive multilevel subset simulation with selective refinement

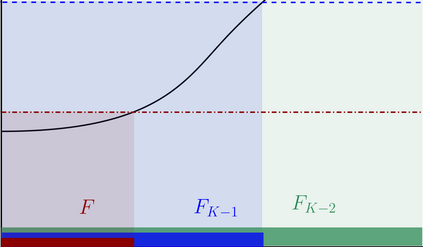
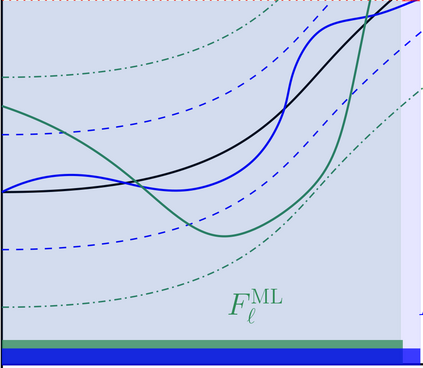
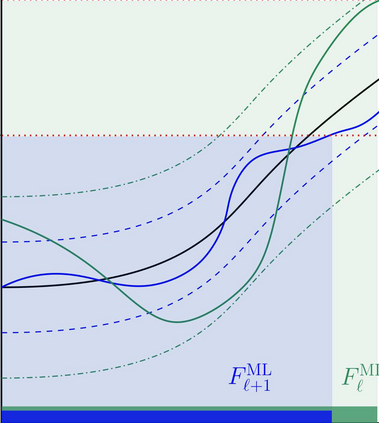
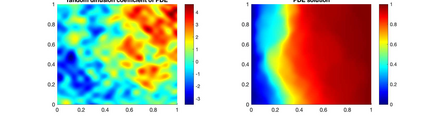
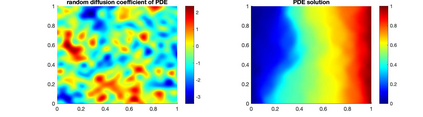
In this work we propose an adaptive multilevel version of subset simulation to estimate the probability of rare events for complex physical systems. Given a sequence of nested failure domains of increasing size, the rare event probability is expressed as a product of conditional probabilities. The proposed new estimator uses different model resolutions and varying numbers of samples across the hierarchy of nested failure sets. In order to dramatically reduce the computational cost, we construct the intermediate failure sets such that only a small number of expensive high-resolution model evaluations are needed, whilst the majority of samples can be taken from inexpensive low-resolution simulations. A key idea in our new estimator is the use of a posteriori error estimators combined with a selective mesh refinement strategy to guarantee the critical subset property that may be violated when changing model resolution from one failure set to the next. The efficiency gains and the statistical properties of the estimator are investigated both theoretically via shaking transformations, as well as numerically. On a model problem from subsurface flow, the new multilevel estimator achieves gains of more than a factor 200 over standard subset simulation for a practically relevant relative error of 25%.