The Power of Populations in Decentralized Bandits

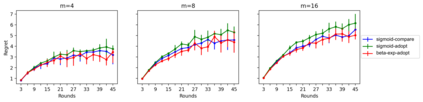
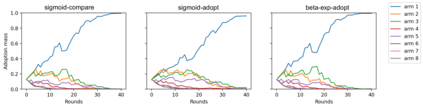
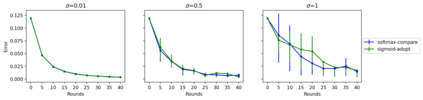
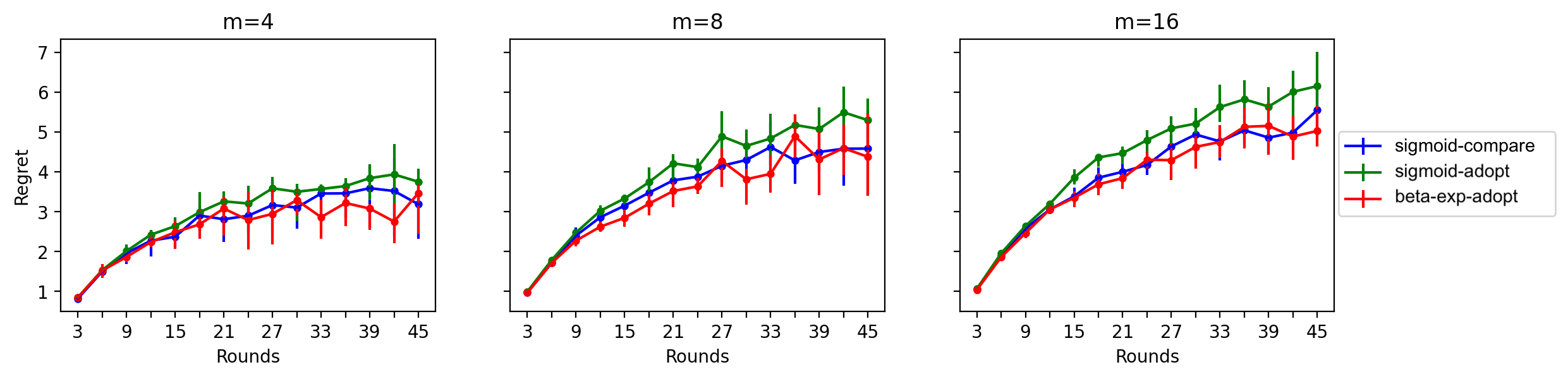
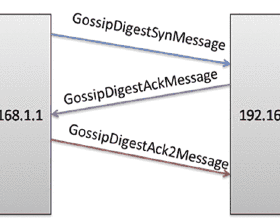
We study a cooperative multi-agent bandit setting in the distributed GOSSIP model: in every round, each of $n$ agents chooses an action from a common set, observes the action's corresponding reward, and subsequently exchanges information with a single randomly chosen neighbor, which informs its policy in the next round. We introduce and analyze several families of fully-decentralized local algorithms in this setting under the constraint that each agent has only constant memory. We highlight a connection between the global evolution of such decentralized algorithms and a new class of "zero-sum" multiplicative weights update methods, and we develop a general framework for analyzing the population-level regret of these natural protocols. Using this framework, we derive sublinear regret bounds for both stationary and adversarial reward settings. Moreover, we show that these simple local algorithms can approximately optimize convex functions over the simplex, assuming that the reward distributions are generated from a stochastic gradient oracle.