On Distributed Computation of the Minimum Triangle Edge Transversal

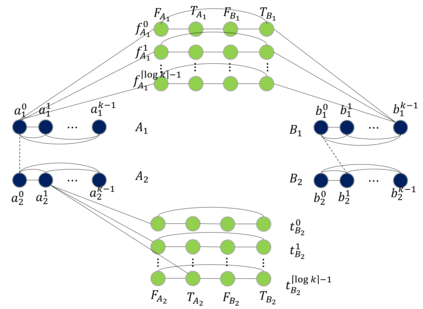
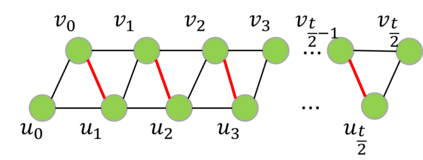
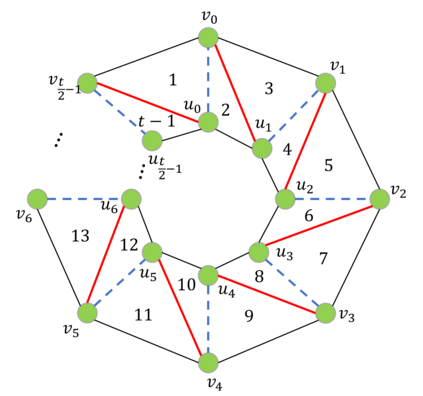
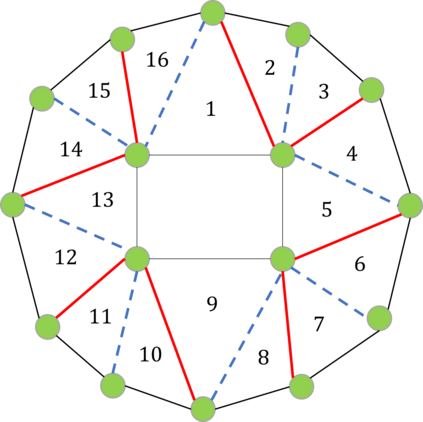
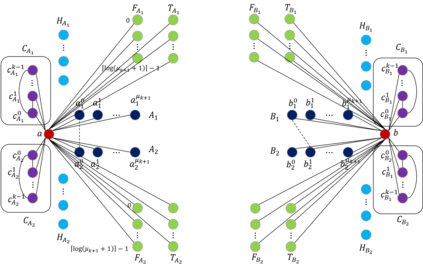
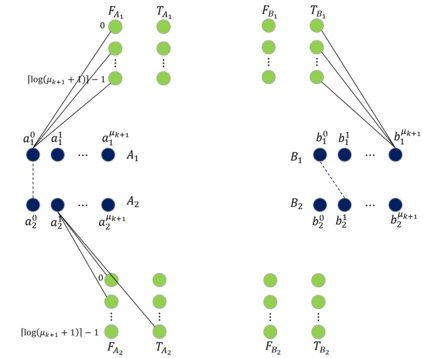
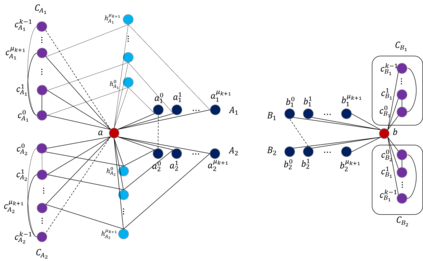
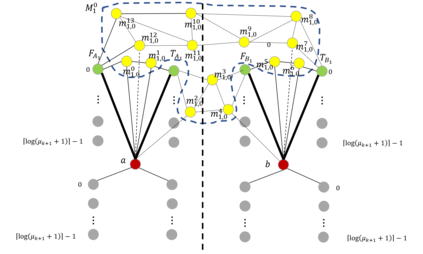
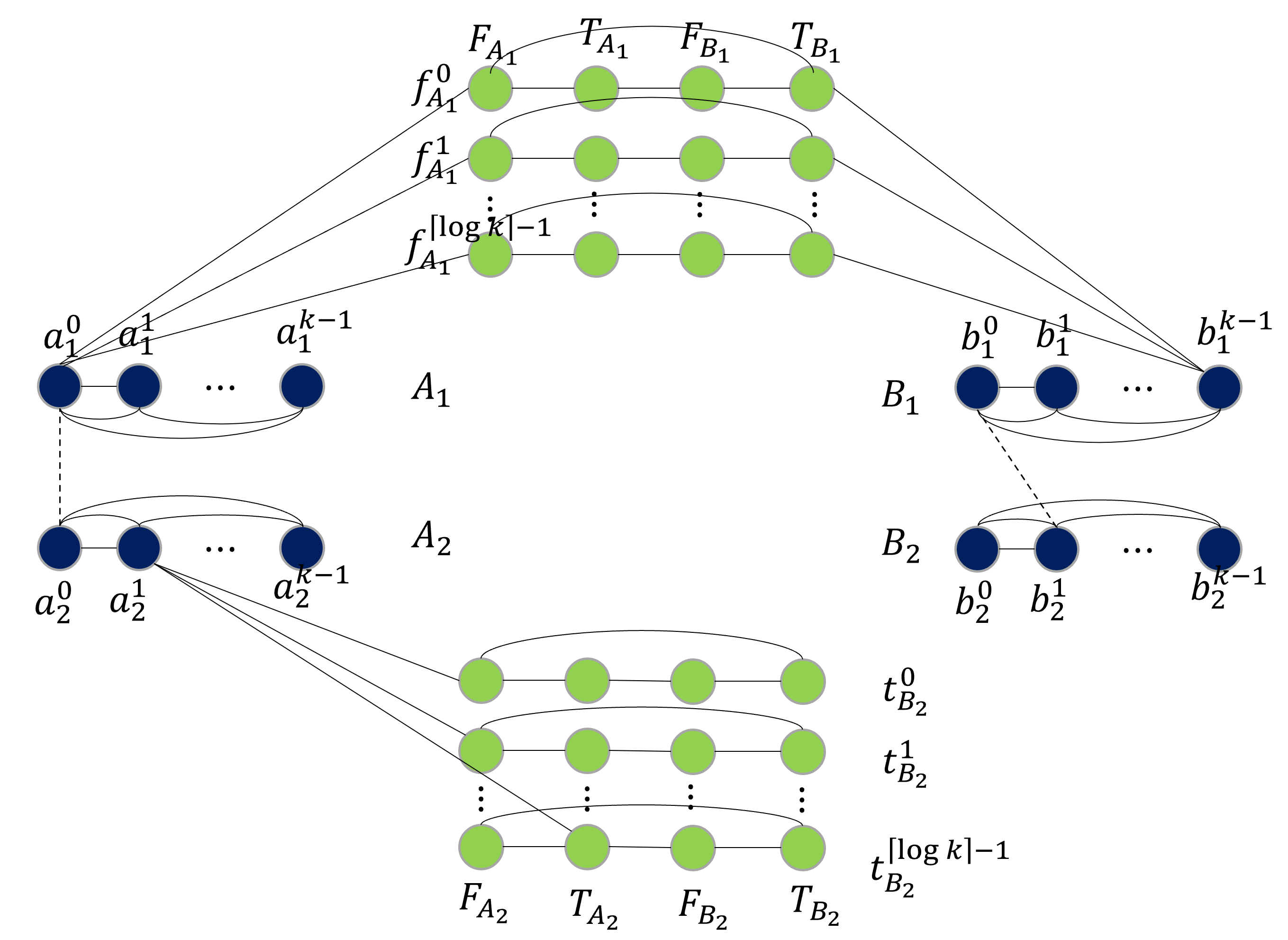
The distance of a graph from being triangle-free is a fundamental graph parameter, counting the number of edges that need to be removed from a graph in order for it to become triangle-free. Its corresponding computational problem is the classic minimum triangle edge transversal problem, and its normalized value is the baseline for triangle-freeness testing algorithms. While triangle-freeness testing has been successfully studied in the distributed setting, computing the distance itself in a distributed setting is unknown, to the best of our knowledge, despite being well-studied in the centralized setting. This work addresses the computation of the minimum triangle edge transversal in distributed networks. We show with a simple warm-up construction that this is a global task, requiring $\Omega(D)$ rounds even in the $\mathsf{LOCAL}$ model with unbounded messages, where $D$ is the diameter of the network. However, we show that approximating this value can be done much faster. A $(1+\epsilon)$-approximation can be obtained in $\text{poly}\log{n}$ rounds, where $n$ is the size of the network graph. Moreover, faster approximations can be obtained, at the cost of increasing the approximation factor to roughly 3, by a reduction to the minimum hypergraph vertex cover problem. With a time overhead of the maximum degree $\Delta$, this can also be applied to the $\mathsf{CONGEST}$ model, in which messages are bounded. Our key technical contribution is proving that computing an exact solution is ``as hard as it gets'' in $\mathsf{CONGEST}$, requiring a near-quadratic number of rounds. Because this problem is an edge selection problem, as opposed to previous lower bounds that were for node selection problems, major challenges arise in constructing the lower bound, requiring us to develop novel ingredients.