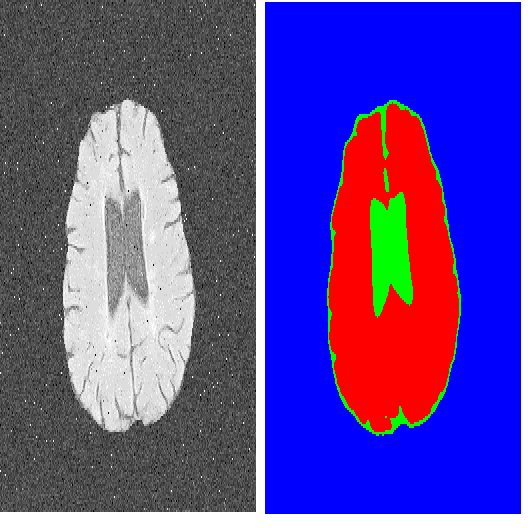
In this paper, we propose a multi-stage image segmentation framework that incorporates a weighted difference of anisotropic and isotropic total variation (AITV). The segmentation framework generally consists of two stages: smoothing and thresholding, thus referred to as SaT. In the first stage, a smoothed image is obtained by an AITV-regularized Mumford-Shah (MS) model, which can be solved efficiently by the alternating direction method of multipliers (ADMM) with a closed-form solution of a proximal operator of the $\ell_1 -\alpha \ell_2$ regularizer. Convergence of the ADMM algorithm is analyzed. In the second stage, we threshold the smoothed image by $k$-means clustering to obtain the final segmentation result. Numerical experiments demonstrate that the proposed segmentation framework is versatile for both grayscale and color images, efficient in producing high-quality segmentation results within a few seconds, and robust to input images that are corrupted with noise, blur, or both. We compare the AITV method with its original convex and nonconvex TV$^p (0<p<1)$ counterparts, showcasing the qualitative and quantitative advantages of our proposed method.
翻译:在本文中,我们提出了一个多阶段图像分割框架(AITV),其中包含厌食和异地总变异的加权差异(AITV),分解框架一般分为两个阶段:平滑和阈值,因此称为SAT。在第一阶段,由AITV正规化的Mumford-Shah(MS)模型获得的平滑图像。 通过乘数交替方向法(ADMMM)可以有效解决,而美元1 - alpha\ ell_2$的准操作器的闭式解决方案。分析ADMM算法的趋同。在第二阶段,我们将平滑图像以$-单位组合为门槛,以获得最后的分解结果。数字实验表明,拟议的分解框架既适合灰度图像和彩色图像,也能在几秒钟内产生高质量分解结果,又能以噪音、模糊或两者都损坏的输入图像。我们将AITV方法与最初的CUV$(OV1)和不高质技术(OV1)对等工具进行比较。