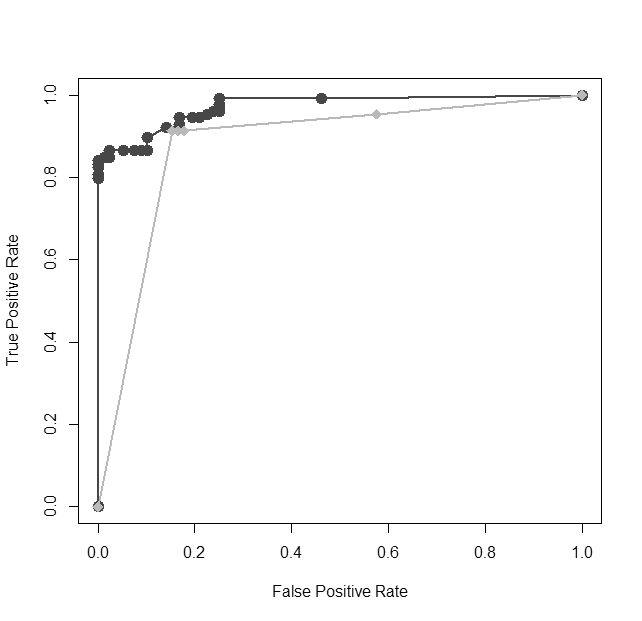
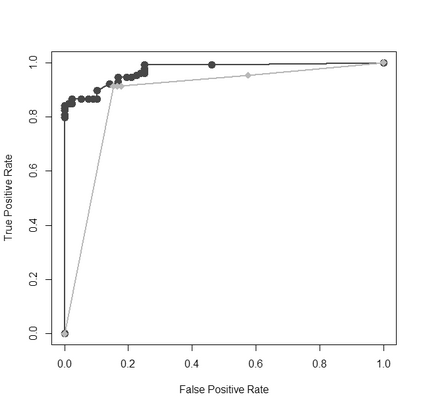
We introduce a Bayesian framework for mixed-type multivariate regression using shrinkage priors. Our method enables joint analysis of mixed continuous and discrete outcomes and facilitates variable selection where the number of covariates $p$ may be larger than sample size $n$. Our model can be implemented with a Gibbs sampling algorithm where all conditional distributions are tractable, leading to a simple one-step estimation procedure. We derive the posterior contraction rate for the one-step estimator when $p$ grows subexponentially with respect to $n$. We further establish that subexponential growth is both a necessary and a sufficient condition for the one-step estimator to achieve posterior consistency. We then introduce a two-step variable selection approach that is suitable for large $p$. We prove that our two-step algorithm possesses the sure screening property. Moreover, our two-step estimator can provably achieve posterior contraction even when $p$ grows exponentially in $n$, thus overcoming a limitation of the one-step estimator. Numerical experiments and analyses of real datasets demonstrate the ability of our joint modeling approach to improve predictive accuracy and identify significant variables in multivariate mixed response models. R codes to implement our method are available at https://github.com/raybai07/MtMBSP.
翻译:暂无翻译